题目内容
已知数列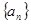 是首项
是首项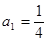 的等比数列,其前
的等比数列,其前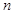 项和
项和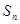 中
中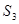 ,
,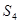 ,
,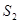 成
成
等差数列,
(1)求数列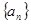 的通项公式;
的通项公式;
(2)设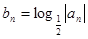 ,若
,若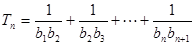 ,求证:
,求证: .
.
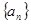 是首项
是首项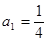 的等比数列,其前
的等比数列,其前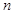 项和
项和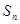 中
中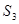 ,
,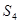 ,
,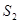 成
成等差数列,
(1)求数列
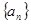 的通项公式;
的通项公式;(2)设
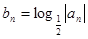 ,若
,若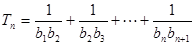 ,求证:
,求证: .
.(1)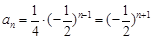 (2)见解析
(2)见解析
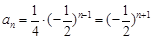 (2)见解析
(2)见解析(1)要注意讨论q=1和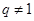 ,当q=1时,不成立;
,当q=1时,不成立;
当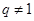 时,由
时,由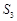 ,
,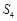 ,
,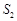 成等差数列得可建立关于q的方程,可求出q的值.
成等差数列得可建立关于q的方程,可求出q的值.
通项公式确定.
(2)在(1)的基础上可知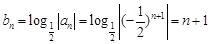 ,
,
所以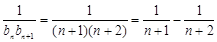 ,因而要考虑采用裂项求和的方法.求出Tn,然后再利用研究数列单调性的方法研究数列的单调性进而确定其最值.
,因而要考虑采用裂项求和的方法.求出Tn,然后再利用研究数列单调性的方法研究数列的单调性进而确定其最值.
解:(1)若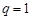 ,则
,则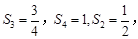 显然
显然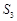 ,
,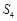 ,
,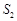 不构成等差数列.--2分
不构成等差数列.--2分
∴ , 当
, 当 时,由
时,由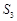 ,
,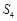 ,
,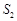 成等差数列得
成等差数列得
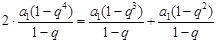
∴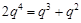
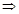

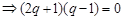 ,
,
∵ ∴
∴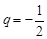 -----------5分
-----------5分
∴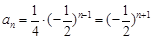 --------------6分
--------------6分
(2)∵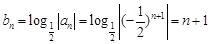
∴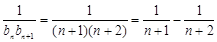 ------------8分
------------8分
∴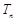 =
=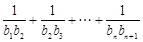
=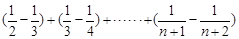
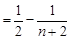 ---------11分
---------11分
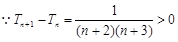 ,
,
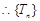 是递增数列.
是递增数列.
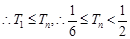 . ------------14分
. ------------14分
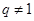 ,当q=1时,不成立;
,当q=1时,不成立;当
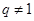 时,由
时,由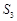 ,
,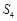 ,
,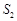 成等差数列得可建立关于q的方程,可求出q的值.
成等差数列得可建立关于q的方程,可求出q的值.通项公式确定.
(2)在(1)的基础上可知
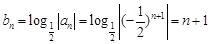 ,
,所以
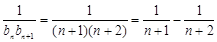 ,因而要考虑采用裂项求和的方法.求出Tn,然后再利用研究数列单调性的方法研究数列的单调性进而确定其最值.
,因而要考虑采用裂项求和的方法.求出Tn,然后再利用研究数列单调性的方法研究数列的单调性进而确定其最值.解:(1)若
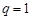 ,则
,则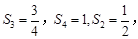 显然
显然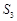 ,
,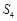 ,
,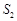 不构成等差数列.--2分
不构成等差数列.--2分∴
 , 当
, 当 时,由
时,由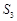 ,
,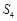 ,
,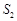 成等差数列得
成等差数列得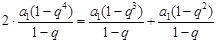
∴
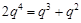
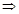

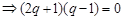 ,
,∵
 ∴
∴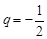 -----------5分
-----------5分∴
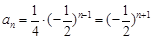 --------------6分
--------------6分(2)∵
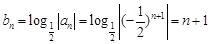
∴
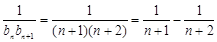 ------------8分
------------8分∴
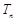 =
=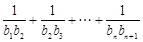
=
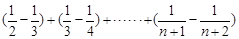
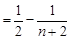 ---------11分
---------11分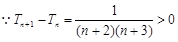 ,
,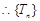 是递增数列.
是递增数列.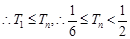 . ------------14分
. ------------14分
练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
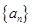 中,
中,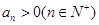 ,公比
,公比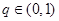 ,且
,且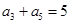 ,又
,又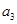 与
与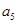 的等比中项为2.
的等比中项为2.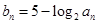 ,数列
,数列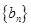 的前
的前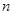 项和为
项和为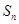 ,求数列
,求数列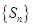 的通项公式;
的通项公式;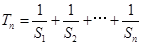 ,求
,求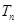 .
.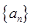 ,其前
,其前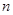 项和为
项和为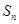 ,若
,若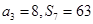 ,则此样本的中位数是( )
,则此样本的中位数是( )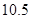
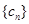 ,其中
,其中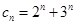 ,且数列
,且数列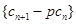 为等比数列,求常数p;
为等比数列,求常数p;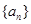 、
、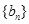 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,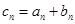 ,证明:数列
,证明:数列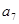 等于()
等于()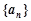 的前4项和为10,且
的前4项和为10,且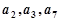 成等比数列.
成等比数列. ;
;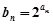 ,求数列
,求数列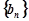 的前
的前 项和
项和 .
.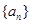 中,已知
中,已知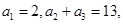 则
则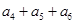 等于( )
等于( )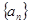 中,
中,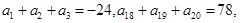 则此数列的前
则此数列的前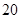 项和 _________.
项和 _________.