题目内容
已知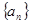 为等比数列,
为等比数列,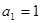 ,
,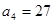 ,
,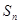 为等差数列
为等差数列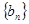 的前
的前 项和,
项和,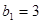 ,
,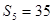 。
。
(I)求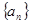 和
和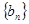 的通项公式;
的通项公式;
(II)设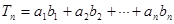 ,求
,求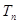 。
。
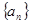 为等比数列,
为等比数列,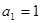 ,
,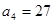 ,
,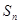 为等差数列
为等差数列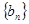 的前
的前 项和,
项和,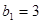 ,
,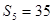 。
。(I)求
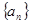 和
和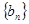 的通项公式;
的通项公式;(II)设
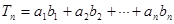 ,求
,求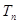 。
。 解:(I)由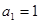 ,
,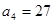 ,可得
,可得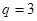 。
。
所以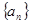 的通项公式
的通项公式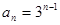 (2分)
(2分)
由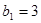 ,
,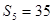 ,可得
,可得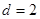 。
。
所以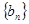 的通项公式
的通项公式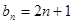 。(5分)
。(5分)
(II)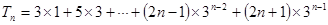 ①
①
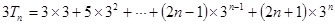 ②
②
①-②得: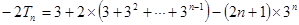 (7分)
(7分)
整理得: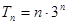 (8分)
(8分)
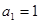 ,
,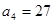 ,可得
,可得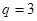 。
。所以
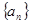 的通项公式
的通项公式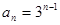 (2分)
(2分)由
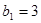 ,
,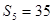 ,可得
,可得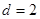 。
。所以
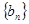 的通项公式
的通项公式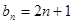 。(5分)
。(5分)(II)
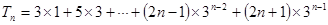 ①
①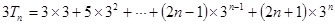 ②
②①-②得:
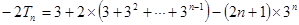 (7分)
(7分)整理得:
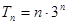 (8分)
(8分)本试题主要是考查了等差数列和等比数列的通项公式的求解以及错位相减法的求和的综合运用。
(1)根据已知条件得到通项公式的关系式得到基本元素的值,然后写出其公式。
(2)在第一问的基础上,结合等比数列的求和的方法来求解数列的前n项和的值。
(1)根据已知条件得到通项公式的关系式得到基本元素的值,然后写出其公式。
(2)在第一问的基础上,结合等比数列的求和的方法来求解数列的前n项和的值。

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
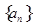 的前
的前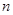 项和为
项和为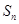 ,且
,且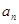 是
是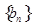 中,
中,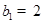 ,点
,点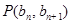 在直线
在直线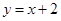 上.
上.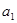 和
和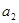 的值;
的值;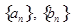 的通项
的通项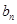 ;
;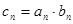 ,求数列
,求数列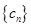 的前n项和
的前n项和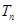 .
.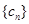 ,其中
,其中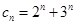 ,且数列
,且数列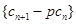 为等比数列,求常数p;
为等比数列,求常数p;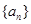 、
、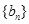 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,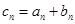 ,证明:数列
,证明:数列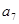 等于()
等于()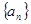 的前三项与数列
的前三项与数列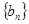 的前三项对应相同,且
的前三项对应相同,且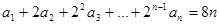 对任意的
对任意的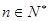 都成立,数列
都成立,数列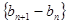 是等差数列
是等差数列
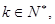 使得
使得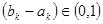 ?请说明理由。
?请说明理由。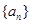 中,已知
中,已知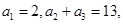 则
则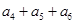 等于( )
等于( )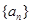 、
、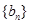 的前
的前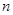 项和的比
项和的比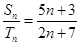 ,则
,则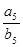 的值是 .
的值是 . :
: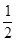 ,
, ,
,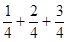 ,
, ,…,那么数列
,…,那么数列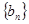 =
=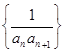 前n项和为( )
前n项和为( )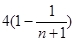
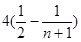

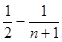
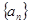 中,
中,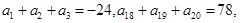 则此数列的前
则此数列的前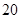 项和 _________.
项和 _________.