题目内容
12.已知四面体ABCD中,每个面都有两条边长为3,有一边为2,则四面体ABCD外接球的表面积为11π.分析 考虑一个长方体ABCD-A1B1C1D1,其四个顶点就构成一个四面体AB1CD1 恰好就是每个三角形边长为3,3,2,则四面体的外接球即为长方体的外接球,进而计算出其外接球的直径,可得外接球的表面积.
解答 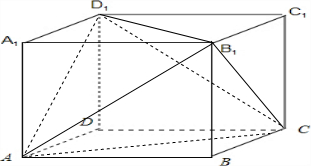 解:设长方体ABCD-A1B1C1D1 的长宽高分别是a,b,c,其四个顶点就构成一个四面体AB1CD1 满足每个面的边长为3,3,2,
解:设长方体ABCD-A1B1C1D1 的长宽高分别是a,b,c,其四个顶点就构成一个四面体AB1CD1 满足每个面的边长为3,3,2,
则a2+b2=9,b2+c2=9,c2+a2=4,
所以a2+b2+c2=11,
即长方体的外接球直径2R=$\sqrt{11}$,
故外接球的表面积S=4πR2=11π,
故答案为:11π.
点评 在求一个几何体的外接球表面积(或体积)时,关键是求出外接球的半径,我们通常有如下办法:①构造三角形,解三角形求出R;②找出几何体上到各顶点距离相等的点,即球心,进而求出R;③将几何体补成一个长方体,其对角线即为球的直径,进而求出R.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
14.某程序框如图所示,若输出的S=57,则判断框内应为( )


| A. | k>6? | B. | k>5? | C. | k>4? | D. | k>3? |
4.袋内有红、白、黑球各3,2,1个,从中任取两个,则互斥而不对立的事件是( )
| A. | 至少有一个白球;都是白球 | B. | 至少一个白球;红,黑球各一个 | ||
| C. | 至少有一个白球;至少有一个红球 | D. | 恰有一个白球;一个白球一个黑球 |