题目内容
2.已知函数y=f(x)(x∈(-∞,-2)∪(2,+∞)),在其图象上任取一点P(x,y)都满足方程x2-4y2=4.①函数y=f(x)一定具有奇偶性;
②函数y=f(x)在(-∞,-2)是单调函数;
③?x0∈(-∞,-2)∪(2,+∞),使x<2f(x);
④?x∈(-∞,-2)∪(2,+∞),使|x|>2f(x);
以上说法正确的序号是③④.
分析 根据条件作出满足条件的函数图象,同时作出渐近线方程y=±$\frac{1}{2}$x,通过图象观察可得函数的奇偶性和单调性即可判断①,②;再由双曲线的性质和图象,即可判断③,④.
解答 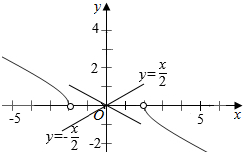 解:满足方程x2-4y2=4的函数图象为双曲线的一部分,
解:满足方程x2-4y2=4的函数图象为双曲线的一部分,
如图,函数y=f(x)对应的图象为2,4象限部分的图象,
或1,3象限的图象,可能不关于原点对称或y轴对称,
则①不正确;
对于②,由图象可得函数y=f(x)在(-∞,-2)
可能是减函数或增函数,不单调,则②不正确;
对于③,由图可知③正确;
对于④,由于图象上任一点P(x,y)满足方程x2-4y2=4,
则?x∈(-∞,-2)∪(2,+∞),由图象可得|x|>2f(x),则④正确.
故答案为:③④.
点评 本题主要考查函数奇偶性和单调性的判断,图象和渐近线的关系,利用双曲线的图象是解决本题的关键.

练习册系列答案
相关题目
17.过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,若|AF|=5,则|BF|=( )
| A. | $\frac{1}{4}$ | B. | 1 | C. | $\frac{5}{4}$ | D. | 2 |
12.曲线$y=\frac{x^2}{lnx}$在点(e,e2)处的切线与直线x+ay=1垂直,则实数a的值为( )
| A. | -$\frac{1}{e}$ | B. | e | C. | $\frac{1}{e}$ | D. | -e |
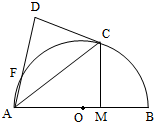 如图,AB是圆O的直径,C、F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M.若圆O的半径为1,∠BAC=30°,则DF•AM=$\frac{3}{4}$.
如图,AB是圆O的直径,C、F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M.若圆O的半径为1,∠BAC=30°,则DF•AM=$\frac{3}{4}$.