题目内容
3.已知抛物线y=x2,点A、B的坐标分别为(2,-1)、(3,1),在抛物线上求一点P使△ABP的面积最小并求出最小面积.分析 求出直线AB的斜率,然后求出函数的导数利用导数值与KAB相等,求出切点坐标,然后求出三角形的高,即可求解三角形的面积的最小值.
解答 S△ABC解:由题意可知KAB=$\frac{1+1}{3-2}$=2,抛物线y=x2,点A、B的坐标分别为(2,-1)、(3,1),在抛物线上求一点P使△ABP的面积最小,这点就是与AB平行与抛物线相切时的切点坐标,
设切点为(a,a2),则y=x2,可得y′=2x,y′|x=a=2a,2a=2,解得a=1,
切点坐标(1,1),直线AB:y-1=2(x-3),可得2x-y-5=0.切点到直线的距离为:d=$\frac{|2-1-5|}{\sqrt{{2}^{2}+({-1)}^{2}}}$=$\frac{4}{\sqrt{5}}$,
|AB|=$\sqrt{(3-2)^{2}+(1+1)^{2}}$=$\sqrt{5}$.
${S}_{△ABC}=\frac{1}{2}\left|AB\right|d$=$\frac{1}{2}×\sqrt{5}×\frac{4}{\sqrt{5}}$=2.
所求面积的最小值为:2,此时P(1,1).
点评 本题考查函数的导数以及三角形的面积的求法,考查转化思想以及计算能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
5.设集合U={1,2,3,4,5,6},A={x∈N|1≤x≤3},则∁UA=( )
| A. | U | B. | {1,2,3} | C. | {4,5,6} | D. | {1,3,4,5,6} |
15.已知f(x)是定义在R上的奇函数,且f(x-2)=f(x+2),当0<x<2时,f(x)=1-log2(x+1),则当0<x<4时,不等式(x-2)f(x)>0的解集是( )
| A. | (0,1)∪(2,3) | B. | (0,1)∪(3,4) | C. | (1,2)∪(3,4) | D. | (1,2)∪(2,3) |
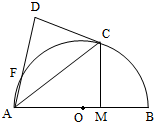 如图,AB是圆O的直径,C、F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M.若圆O的半径为1,∠BAC=30°,则DF•AM=$\frac{3}{4}$.
如图,AB是圆O的直径,C、F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M.若圆O的半径为1,∠BAC=30°,则DF•AM=$\frac{3}{4}$.