题目内容
【题目】如图,在三棱柱![]() 中,四边形
中,四边形![]() ,
,![]() 均为正方形,且
均为正方形,且![]() ,M为
,M为![]() 的中点,N为
的中点,N为![]() 的中点.
的中点.
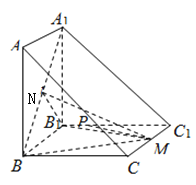
(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)设P是棱![]() 上一点,若直线PM与平面
上一点,若直线PM与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值
的值
【答案】(1)证明过程见详解;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先取![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,根据面面平行的判定定理,得到平面
,根据面面平行的判定定理,得到平面![]() 平面
平面![]() ,进而可得
,进而可得![]() 平面ABC;
平面ABC;
(2)先由题意,得到![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() 边长为
边长为![]() ,分别求出平面
,分别求出平面![]() 和平面
和平面![]() 的一个法向量,根据向量夹角公式,求解,即可得出结果;
的一个法向量,根据向量夹角公式,求解,即可得出结果;
(3)先设![]() ,得到
,得到![]() ,根据空间向量的夹角公式,列出等式求解,即可得出结果.
,根据空间向量的夹角公式,列出等式求解,即可得出结果.
(1)取![]() 中点为
中点为![]() ,连接
,连接![]() ,
,![]() ,
,
因为![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() 平面ABC;
平面ABC;
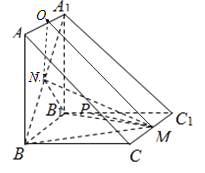
(2)因为四边形![]() ,
,![]() 均为正方形,所以
均为正方形,所以![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,设
轴建立如图所示的空间直角坐标系,设![]() 边长为
边长为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
因此![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则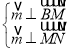 ,所以
,所以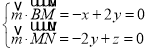 ,令
,令![]() ,则
,则![]() ,
,
因此![]() ;
;
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则 ,所以
,所以 ,令
,令![]() ,则
,则![]() ,
,
因此![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,
,
则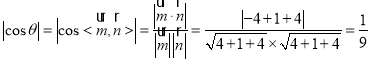 ,
,
所以![]() ;
;
(3)因为![]() 是棱
是棱![]() 上一点,设
上一点,设![]() ,则
,则![]() ,
,
所以![]() ,
,
由(2)知,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,记直线
,记直线![]() 与平面
与平面![]() 所成角为
所成角为![]()
则有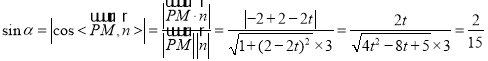 ,
,
整理得![]() ,解得
,解得![]() 或
或![]() (舍)
(舍)
所以![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案【题目】已知某校运动会男生组田径综合赛以选手三项运动的综合积分高低决定排名.具体积分规则如表1所示,某代表队四名男生的模拟成绩如表2.
表1 田径综合赛项目及积分规则
项目 | 积分规则 |
| 以 |
跳高 | 以 |
掷实心球 | 以 |
表2 某队模拟成绩明细
姓名 | 100米跑(秒) | 跳高(米) | 掷实心球(米) |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根据模拟成绩,该代表队应选派参赛的队员是:( )
A.甲B.乙C.丙D.丁