Question

选修4-1：几何证明选讲．
如图，AB是⊙O的一条切线，切点为B，ADE、CFD、CGE都是⊙O的割线，已知AC=AB．证明：
（1）AD•AE=AC²；
（2）FG∥AC．

Answer 1

分析：（1）利用切线长与割线长的关系及AB=AC 进行证明．
（2）利用成比例的线段证明角相等、三角形相似，得到同位角角相等，从而两直线平行．

解答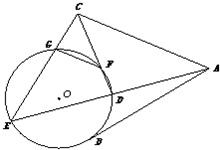：证明：（1）∵AB是⊙O的一条切线，切点为B，ADE，CFD，CGE都是⊙O的割线，
∴AB²=AD•AE，∵AB=AC，∴AD•AE=AC²．

（2）由（1）有

AD

AC

=

AC

AE

，∵∠EAC=∠DAC，
∴△ADC∽△ACE，∴∠ADC=∠ACE，∵∠ADC=∠EGF，
∴∠EGF=∠ACE，
∴GF∥AC．

点评：本题考查圆的切线、割线长的关系，平面的基本性质．解决这类问题的常用方法是利用成比例的线段证明角相等、三角形相似等知识．