题目内容
已知离心率为 的椭圆C1的顶点A1,A2恰好是双曲线
的椭圆C1的顶点A1,A2恰好是双曲线 的左右焦点,点P是椭圆上不同于A1,A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2.
的左右焦点,点P是椭圆上不同于A1,A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2.(Ⅰ)求椭圆C1的标准方程;
(Ⅱ)试判断k1•k2的值是否与点P的位置有关,并证明你的结论;
(Ⅲ)当
 时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为
时,圆C2:x2+y2-2mx=0被直线PA2截得弦长为 ,求实数m的值.
,求实数m的值.设计意图:考察直线上两点的斜率公式、直线与圆相交、垂径定理、双曲线与椭圆的几何性质等知识,考察学生用待定系数法求椭圆方程等解析几何的基本思想与运算能力、探究能力和推理能力.第(Ⅱ)改编自人教社选修2-1教材P39例3.
【答案】分析:(Ⅰ)先利用椭圆C1的顶点A1,A2恰好是双曲线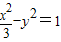 的左右焦点求出顶点A1,A2的坐标,再利用离心率为
的左右焦点求出顶点A1,A2的坐标,再利用离心率为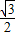 即可求椭圆C1的标准方程;
即可求椭圆C1的标准方程;
(Ⅱ)直接利用两点坐标求出k1•k2的值即可判断k1•k2的值是否与点P的位置有关;
(Ⅲ)先利用(Ⅱ)的结论求出直线PA2的方程,再利用圆心到直线的距离以及弦长和半径之间的关系即可求实数m的值.
解答:解:(Ⅰ)双曲线 的左右焦点为(±2,0)
的左右焦点为(±2,0)
即A1,A2的坐标分别为(-2,0),(2,0).(1分)
所以设椭圆C1的标准方程为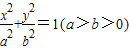 ,则a=2,(2分)
,则a=2,(2分)
且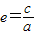 =
=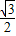 ,所以
,所以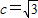 ,从而b2=a2-c2=1,(4分)
,从而b2=a2-c2=1,(4分)
所以椭圆C1的标准方程为 .(5分)
.(5分)
(Ⅱ)设P(x,y)则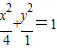 ,即
,即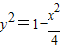 =
=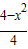 (6分)
(6分)
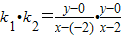 =
= =
=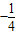 .(8分)
.(8分)
所以k1•k2的值与点P的位置无关,恒为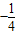 . (9分)
. (9分)
(Ⅲ)由圆C2:x2+y2-2mx=0得(x-m)2+y2=m2,
其圆心为C2(m,0),半径为|m|,(10分)
由(Ⅱ)知当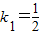 时,
时,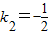 ,
,
故直线PA2的方程为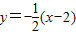 即x+2y-2=0,(11分)
即x+2y-2=0,(11分)
所以圆心为C2(m,0)到直线PA2的距离为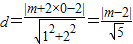 ,
,
又由已知圆C2:x2+y2-2mx=0被直线PA2截得弦长为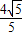 及垂径定理得
及垂径定理得
圆心C2(m,0)到直线PA2的距离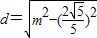 ,
,
所以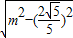 =
=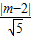 ,即m2+m-2=0,解得m=-2或m=1.(13分)
,即m2+m-2=0,解得m=-2或m=1.(13分)
所以实数m的值为1或-2.(14分).
点评:本题主要考查直线上两点的斜率公式、直线与圆相交、垂径定理、双曲线与椭圆的几何性质等知识,考查学生用待定系数法求椭圆方程等解析几何的基本思想与运算能力、探究能力和推理能力.
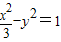 的左右焦点求出顶点A1,A2的坐标,再利用离心率为
的左右焦点求出顶点A1,A2的坐标,再利用离心率为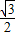 即可求椭圆C1的标准方程;
即可求椭圆C1的标准方程;(Ⅱ)直接利用两点坐标求出k1•k2的值即可判断k1•k2的值是否与点P的位置有关;
(Ⅲ)先利用(Ⅱ)的结论求出直线PA2的方程,再利用圆心到直线的距离以及弦长和半径之间的关系即可求实数m的值.
解答:解:(Ⅰ)双曲线
 的左右焦点为(±2,0)
的左右焦点为(±2,0)即A1,A2的坐标分别为(-2,0),(2,0).(1分)
所以设椭圆C1的标准方程为
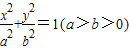 ,则a=2,(2分)
,则a=2,(2分)且
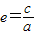 =
=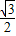 ,所以
,所以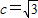 ,从而b2=a2-c2=1,(4分)
,从而b2=a2-c2=1,(4分)所以椭圆C1的标准方程为
 .(5分)
.(5分)(Ⅱ)设P(x,y)则
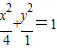 ,即
,即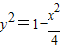 =
=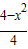 (6分)
(6分)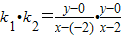 =
= =
=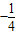 .(8分)
.(8分)所以k1•k2的值与点P的位置无关,恒为
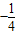 . (9分)
. (9分)(Ⅲ)由圆C2:x2+y2-2mx=0得(x-m)2+y2=m2,
其圆心为C2(m,0),半径为|m|,(10分)
由(Ⅱ)知当
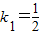 时,
时,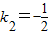 ,
,故直线PA2的方程为
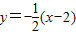 即x+2y-2=0,(11分)
即x+2y-2=0,(11分)所以圆心为C2(m,0)到直线PA2的距离为
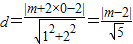 ,
,又由已知圆C2:x2+y2-2mx=0被直线PA2截得弦长为
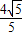 及垂径定理得
及垂径定理得圆心C2(m,0)到直线PA2的距离
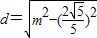 ,
,所以
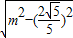 =
=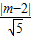 ,即m2+m-2=0,解得m=-2或m=1.(13分)
,即m2+m-2=0,解得m=-2或m=1.(13分)所以实数m的值为1或-2.(14分).
点评:本题主要考查直线上两点的斜率公式、直线与圆相交、垂径定理、双曲线与椭圆的几何性质等知识,考查学生用待定系数法求椭圆方程等解析几何的基本思想与运算能力、探究能力和推理能力.

练习册系列答案
相关题目

 的椭圆C:
的椭圆C: 过(1,
过(1, )
) 的椭圆C:
的椭圆C: +
+ =1(a>b>0)过点M(
=1(a>b>0)过点M( ,1,O是坐标原点.
,1,O是坐标原点. ⊥
⊥ ,判定直线AB与圆O:x2+y2=
,判定直线AB与圆O:x2+y2= 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. 为的椭圆C:
为的椭圆C: (a>b>0)与过点A(5,0),B(0,
(a>b>0)与过点A(5,0),B(0, )的直线有且只有一个公共点M.
)的直线有且只有一个公共点M. ,若存在,求出直线l的方程;若不存在,请说明理由.
,若存在,求出直线l的方程;若不存在,请说明理由. 的椭圆C:
的椭圆C: 的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为
的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为 .
. .试探究
.试探究 的取值范围.
的取值范围.