题目内容
已知离心率为 的椭圆C:
的椭圆C: +
+ =1(a>b>0)过点M(
=1(a>b>0)过点M( ,1,O是坐标原点.
,1,O是坐标原点.(1)求椭圆C的方程;
(2)已知点A、B为椭圆C上相异两点,且
 ⊥
⊥ ,判定直线AB与圆O:x2+y2=
,判定直线AB与圆O:x2+y2= 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
【答案】分析:(1)由 ,能求出椭圆C的方程.
,能求出椭圆C的方程.
(2)设A(x1,y1),B(x2,y2),直线AB的方程为:y=kx+m,由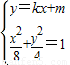 ,得:(1+2k2)x2+4kmx+2m2-8=0,由△=8(8k2-m2+4)>0,知8k2-m2+4>0,由韦达定理得:
,得:(1+2k2)x2+4kmx+2m2-8=0,由△=8(8k2-m2+4)>0,知8k2-m2+4>0,由韦达定理得: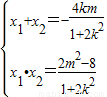 ,y1•y2=(kx1+m)•(kx2+m)=
,y1•y2=(kx1+m)•(kx2+m)=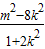 .由
.由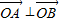 得x1x2+y1y2=0.由圆心到直线的距离
得x1x2+y1y2=0.由圆心到直线的距离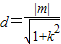 ,能够推导出直线AB与圆O相切.
,能够推导出直线AB与圆O相切.
解答:解:(1)由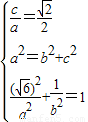 ,解得:
,解得: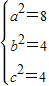 ,故椭圆C的方程为
,故椭圆C的方程为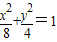 .(4分)
.(4分)
(2)设A(x1,y1),B(x2,y2),直线AB的方程为:y=kx+m,
由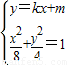 ,得:(1+2k2)x2+4kmx+2m2-8=0,(1分)
,得:(1+2k2)x2+4kmx+2m2-8=0,(1分)
则△=8(8k2-m2+4)>0,即8k2-m2+4>0,
由韦达定理得: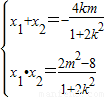 ,(1分)
,(1分)
则y1•y2=(kx1+m)•(kx2+m)
=k2x1x2+km(x1+x2)+m2
=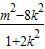 .
.
由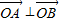 得:
得:
x1x2+y1y2=0,(1分)
即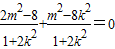 ,化简得:3m2-8k2-8=0,(1分)
,化简得:3m2-8k2-8=0,(1分)
因为圆心到直线的距离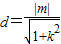 ,(1分)
,(1分)
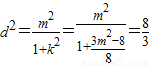 ,
,
而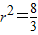 ,∴d2=r2,即d=r.(1分)
,∴d2=r2,即d=r.(1分)
此时直线AB与圆O相切
当直线AB的斜率不存在时,由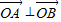 可以计算得A,B的坐标为
可以计算得A,B的坐标为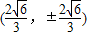 或
或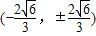 .
.
此时直线AB的方程为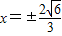 .
.
满足圆心到直线的距离等于半径,即直线AB与圆O相切.(1分)
综上,直线AB与圆O相切.(1分)
点评:本题考查椭圆C的方程,判定直线与圆的位置关系,并证明.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用椭圆性质,合理地进行等价转化.
 ,能求出椭圆C的方程.
,能求出椭圆C的方程.(2)设A(x1,y1),B(x2,y2),直线AB的方程为:y=kx+m,由
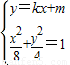 ,得:(1+2k2)x2+4kmx+2m2-8=0,由△=8(8k2-m2+4)>0,知8k2-m2+4>0,由韦达定理得:
,得:(1+2k2)x2+4kmx+2m2-8=0,由△=8(8k2-m2+4)>0,知8k2-m2+4>0,由韦达定理得: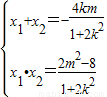 ,y1•y2=(kx1+m)•(kx2+m)=
,y1•y2=(kx1+m)•(kx2+m)=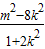 .由
.由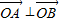 得x1x2+y1y2=0.由圆心到直线的距离
得x1x2+y1y2=0.由圆心到直线的距离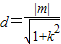 ,能够推导出直线AB与圆O相切.
,能够推导出直线AB与圆O相切.解答:解:(1)由
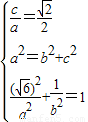 ,解得:
,解得: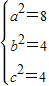 ,故椭圆C的方程为
,故椭圆C的方程为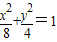 .(4分)
.(4分)(2)设A(x1,y1),B(x2,y2),直线AB的方程为:y=kx+m,
由
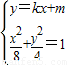 ,得:(1+2k2)x2+4kmx+2m2-8=0,(1分)
,得:(1+2k2)x2+4kmx+2m2-8=0,(1分)则△=8(8k2-m2+4)>0,即8k2-m2+4>0,
由韦达定理得:
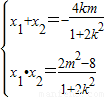 ,(1分)
,(1分)则y1•y2=(kx1+m)•(kx2+m)
=k2x1x2+km(x1+x2)+m2
=
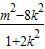 .
.由
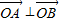 得:
得:x1x2+y1y2=0,(1分)
即
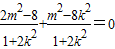 ,化简得:3m2-8k2-8=0,(1分)
,化简得:3m2-8k2-8=0,(1分)因为圆心到直线的距离
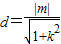 ,(1分)
,(1分)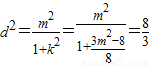 ,
,而
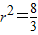 ,∴d2=r2,即d=r.(1分)
,∴d2=r2,即d=r.(1分)此时直线AB与圆O相切
当直线AB的斜率不存在时,由
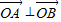 可以计算得A,B的坐标为
可以计算得A,B的坐标为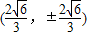 或
或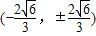 .
.此时直线AB的方程为
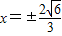 .
.满足圆心到直线的距离等于半径,即直线AB与圆O相切.(1分)
综上,直线AB与圆O相切.(1分)
点评:本题考查椭圆C的方程,判定直线与圆的位置关系,并证明.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用椭圆性质,合理地进行等价转化.

练习册系列答案
相关题目
 的椭圆C:
的椭圆C: 过(1,
过(1, )
) 为的椭圆C:
为的椭圆C: (a>b>0)与过点A(5,0),B(0,
(a>b>0)与过点A(5,0),B(0, )的直线有且只有一个公共点M.
)的直线有且只有一个公共点M. ,若存在,求出直线l的方程;若不存在,请说明理由.
,若存在,求出直线l的方程;若不存在,请说明理由. 的椭圆C:
的椭圆C: 的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为
的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为 .
. .试探究
.试探究 的取值范围.
的取值范围.