题目内容
已知离心率为 的椭圆C:
的椭圆C: 过(1,
过(1, )
)(1)求椭圆C的方程;
(2)是否存在实数m,使得在此椭圆C上存在不同两点关于直线y=4x+m对称,若存在请求出m,若不存在请说明理由.
【答案】分析:(1)由离心率为 的椭圆C:
的椭圆C: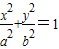 过(1,
过(1, ),知
),知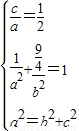 ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程.
(2)假设存在实数m,使得在此椭圆C上存在不同两点关于直线y=4x+m对称.设A(x1,y1),B(x2,y2),AB的中点M(x,y),因为在此椭圆C上存在不同两点关于直线y=4x+m对称,所以 ,再用点差法进行求解.
,再用点差法进行求解.
解答:解:(1)∵离心率为 的椭圆C:
的椭圆C: 过(1,
过(1, ),
),
∴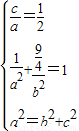 ,解得a2=4,b2=3,c2=1,
,解得a2=4,b2=3,c2=1,
∴椭圆C的方程为
(2)假设存在实数m,使得在此椭圆C上存在不同两点关于直线y=4x+m对称.
设A(x1,y1),B(x2,y2),AB的中点M(x,y),
∵在此椭圆C上存在不同两点关于直线y=4x+m对称,
∴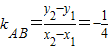 ,
,
∵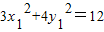 ,
, ,
,
相减得 ,即y1+y2=3(x1+x2),
,即y1+y2=3(x1+x2),
∴y=3x,3x=4x+m,x=-m,y=-3m
而M(x,y)在椭圆内部,则 ,即
,即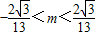 .
.
故存在实数m∈(- ,
, ),使得在此椭圆C上存在不同两点关于直线y=4x+m对称.
),使得在此椭圆C上存在不同两点关于直线y=4x+m对称.
点评:本题考查椭圆方程的求法,考查满足条件的实数的取值范围的求法,综合性强,难度大,具有一定的探索性,对数学思维的要求较高.解题时要注意等价转化思想的合理运用.
 的椭圆C:
的椭圆C: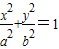 过(1,
过(1, ),知
),知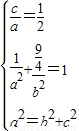 ,由此能求出椭圆C的方程.
,由此能求出椭圆C的方程.(2)假设存在实数m,使得在此椭圆C上存在不同两点关于直线y=4x+m对称.设A(x1,y1),B(x2,y2),AB的中点M(x,y),因为在此椭圆C上存在不同两点关于直线y=4x+m对称,所以
 ,再用点差法进行求解.
,再用点差法进行求解.解答:解:(1)∵离心率为
 的椭圆C:
的椭圆C: 过(1,
过(1, ),
),∴
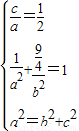 ,解得a2=4,b2=3,c2=1,
,解得a2=4,b2=3,c2=1,∴椭圆C的方程为

(2)假设存在实数m,使得在此椭圆C上存在不同两点关于直线y=4x+m对称.
设A(x1,y1),B(x2,y2),AB的中点M(x,y),
∵在此椭圆C上存在不同两点关于直线y=4x+m对称,
∴
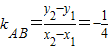 ,
,∵
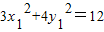 ,
, ,
,相减得
 ,即y1+y2=3(x1+x2),
,即y1+y2=3(x1+x2),∴y=3x,3x=4x+m,x=-m,y=-3m
而M(x,y)在椭圆内部,则
 ,即
,即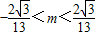 .
.故存在实数m∈(-
 ,
, ),使得在此椭圆C上存在不同两点关于直线y=4x+m对称.
),使得在此椭圆C上存在不同两点关于直线y=4x+m对称.点评:本题考查椭圆方程的求法,考查满足条件的实数的取值范围的求法,综合性强,难度大,具有一定的探索性,对数学思维的要求较高.解题时要注意等价转化思想的合理运用.

练习册系列答案
相关题目
 的椭圆C:
的椭圆C: +
+ =1(a>b>0)过点M(
=1(a>b>0)过点M( ,1,O是坐标原点.
,1,O是坐标原点. ⊥
⊥ ,判定直线AB与圆O:x2+y2=
,判定直线AB与圆O:x2+y2= 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. 为的椭圆C:
为的椭圆C: (a>b>0)与过点A(5,0),B(0,
(a>b>0)与过点A(5,0),B(0, )的直线有且只有一个公共点M.
)的直线有且只有一个公共点M. ,若存在,求出直线l的方程;若不存在,请说明理由.
,若存在,求出直线l的方程;若不存在,请说明理由. 的椭圆C:
的椭圆C: 的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为
的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为 .
. .试探究
.试探究 的取值范围.
的取值范围.