题目内容
已知离心率为 的椭圆C:
的椭圆C: 的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为
的左焦点为F,上顶点为E,直线EF截圆x2+y2=1所得弦长为 .
.(1)求椭圆C的方程;
(2)过D(-2,0)的直线l与椭圆C交于不同的两点A、B,
 .试探究
.试探究 的取值范围.
的取值范围.
【答案】分析:(1)由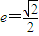 ,得c=b,直线EF的方程为:x-y=-b,由题意原点O 到直线EF的距离为
,得c=b,直线EF的方程为:x-y=-b,由题意原点O 到直线EF的距离为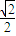 ,知b=1,a2=2,由此能求出椭圆C的方程.
,知b=1,a2=2,由此能求出椭圆C的方程.
(2)若直线l∥x轴,则A、B分别是长轴的两个端点,M在原点O处,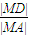 =
=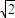 ;若直线l与x轴不平行时,设直线l的方程为:x=my-2,设A(x1,y1)、B(x2,y2)、M(x,y),由
;若直线l与x轴不平行时,设直线l的方程为:x=my-2,设A(x1,y1)、B(x2,y2)、M(x,y),由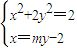 得:(m2+2)y2-4my+2=0,由△=(-4m)2-8(m2+2)>0,知m2>2,
得:(m2+2)y2-4my+2=0,由△=(-4m)2-8(m2+2)>0,知m2>2,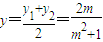 ,由此能推导出
,由此能推导出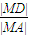
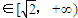 .
.
解答:解:(1)由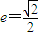 ,得c=b,直线EF的方程为:x-y=-b,
,得c=b,直线EF的方程为:x-y=-b,
由题意原点O 到直线EF的距离为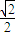 ,
,
∴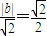 ,
,
∴b=1,a2=2,
∴椭圆C的方程是: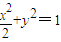 .…(4分)
.…(4分)
(2)①若直线l∥x轴,则A、B分别是长轴的两个端点,M在原点O处,
∴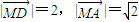 ,
,
∴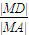 =
=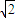 .…(6分)
.…(6分)
②若直线l与x轴不平行时,
设直线l的方程为:x=my-2,
并设A(x1,y1)、B(x2,y2)、M(x,y),
则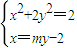 ,
,
得:(m2+2)y2-4my+2=0,(*) …(8分)
∵△=(-4m)2-8(m2+2)>0,
∴m2>2,
由(*)式得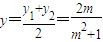 ,
,
∴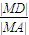 =
=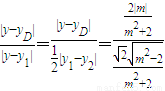 =
= ,
,
∵m2>2,
∴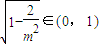 ,
,
∴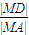
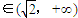
综上,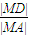
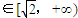 .…(14分)
.…(14分)
点评:本题考查直线和椭圆的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易错点是探究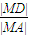 的取值范围时因能力欠缺导致出错,是高考的重点.解题时要认真审题,仔细解答,注意提高解题能力.
的取值范围时因能力欠缺导致出错,是高考的重点.解题时要认真审题,仔细解答,注意提高解题能力.
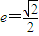 ,得c=b,直线EF的方程为:x-y=-b,由题意原点O 到直线EF的距离为
,得c=b,直线EF的方程为:x-y=-b,由题意原点O 到直线EF的距离为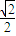 ,知b=1,a2=2,由此能求出椭圆C的方程.
,知b=1,a2=2,由此能求出椭圆C的方程.(2)若直线l∥x轴,则A、B分别是长轴的两个端点,M在原点O处,
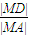 =
=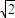 ;若直线l与x轴不平行时,设直线l的方程为:x=my-2,设A(x1,y1)、B(x2,y2)、M(x,y),由
;若直线l与x轴不平行时,设直线l的方程为:x=my-2,设A(x1,y1)、B(x2,y2)、M(x,y),由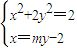 得:(m2+2)y2-4my+2=0,由△=(-4m)2-8(m2+2)>0,知m2>2,
得:(m2+2)y2-4my+2=0,由△=(-4m)2-8(m2+2)>0,知m2>2,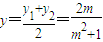 ,由此能推导出
,由此能推导出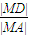
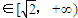 .
.解答:解:(1)由
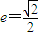 ,得c=b,直线EF的方程为:x-y=-b,
,得c=b,直线EF的方程为:x-y=-b,由题意原点O 到直线EF的距离为
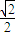 ,
,∴
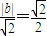 ,
,∴b=1,a2=2,
∴椭圆C的方程是:
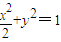 .…(4分)
.…(4分)(2)①若直线l∥x轴,则A、B分别是长轴的两个端点,M在原点O处,
∴
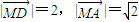 ,
,∴
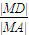 =
=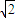 .…(6分)
.…(6分)②若直线l与x轴不平行时,
设直线l的方程为:x=my-2,
并设A(x1,y1)、B(x2,y2)、M(x,y),
则
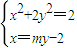 ,
,得:(m2+2)y2-4my+2=0,(*) …(8分)
∵△=(-4m)2-8(m2+2)>0,
∴m2>2,
由(*)式得
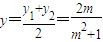 ,
,∴
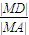 =
=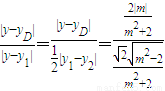 =
= ,
,∵m2>2,
∴
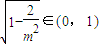 ,
,∴
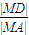
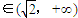
综上,
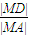
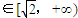 .…(14分)
.…(14分)点评:本题考查直线和椭圆的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易错点是探究
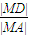 的取值范围时因能力欠缺导致出错,是高考的重点.解题时要认真审题,仔细解答,注意提高解题能力.
的取值范围时因能力欠缺导致出错,是高考的重点.解题时要认真审题,仔细解答,注意提高解题能力. 
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 的椭圆C:
的椭圆C: 过(1,
过(1, )
) 的椭圆C:
的椭圆C: +
+ =1(a>b>0)过点M(
=1(a>b>0)过点M( ,1,O是坐标原点.
,1,O是坐标原点. ⊥
⊥ ,判定直线AB与圆O:x2+y2=
,判定直线AB与圆O:x2+y2= 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. 为的椭圆C:
为的椭圆C: (a>b>0)与过点A(5,0),B(0,
(a>b>0)与过点A(5,0),B(0, )的直线有且只有一个公共点M.
)的直线有且只有一个公共点M. ,若存在,求出直线l的方程;若不存在,请说明理由.
,若存在,求出直线l的方程;若不存在,请说明理由.