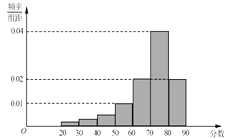
题目内容
【题目】某家庭记录了未使用节水龙头50天的日用水量数据（单位：
）和使用了节水龙头50天的日用水量数据，得到频数分布表如下：
未使用节水龙头50天的日用水量频数分布表
日用水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) | [0.6,0.7) |
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) |
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
（1）作出使用了节水龙头50天的日用水量数据的频率分布直方图；
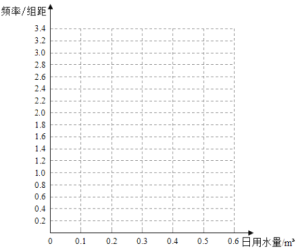
（2）估计该家庭使用节水龙头后，日用水量小于0.3的概率；
（3）估计该家庭用节水龙头后，一年能节省多少水.（一年按365天计算，同一组中的数据以这组数据所在区间中点的值作代表）
【答案】(1)频率分布直方图见详解；(2)0.38；(3)
.
【解析】
（1）由表格数据，分别计算频率和组距的比值，再在频率分布直方图中画出即可；
（2）根据频率分布直方图，算出日用水量小于0.3的长方形面积即可.
（3）先根据频率分布直方图，计算出使用节水龙头后，日均用水量的平均值，结合未使用节水龙头时的日均用水量，即可计算出一年节省的水量.
（1）根据使用节水龙头50天的日用水量频数分布表，可得：
日用水量在区间[0,0.1)的频率为
，频率和组距的比值为
日用水量在区间[0.1,0.2)的频率为
，频率和组距的比值为
日用水量在区间[0.2,0.3)的频率为
，频率和组距的比值为
日用水量在区间[0.3,0.4)的频率为
，频率和组距的比值为
日用水量在区间[0.4,0.5)的频率为
，频率和组距的比值为
日用水量在区间[0.5,0.6)的频率为，频率和组距的比值为
据此绘制频率分布直方图如下所示：
（2）由（1）所求频率分布直方图可知，
日用水量小于0.3的概率为
.
（3）由（1）中所求频率分布直方图，设使用节水龙头后日均用水量为
则
可得
.
根据未使用节水龙头时的日均用水量的频数分布表，设未使用节水龙头日均用水量为
，
则
可得
故使用节水龙头后，每年节省的水量为：
即每年节省水量
.
优学名师名题系列答案
【题目】某部门在十一月份对城市居民进行了主题为空气质量问卷调查，根据每份调查表得到每个调查对象的空气质量评分值（百分制）．现从收到的调查表中随机抽取20份进行统计，得到如图所示的频率分布表：
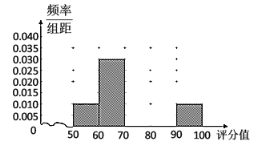
空气质量评分值 | 频数 | 频率 |
[50，60] | 2 |
|
（60.70] | 6 |
|
（70，80] |
|
|
（80，90] | 3 |
|
（90，100] | 2 |
|
（1）请完成题目中的频率分布表，并补全题目中的频率分布直方图；
（2）该部门将邀请被问卷调查的部分居民参加如何提高空气质量的座谈会．在题中抽样统计的这20人中，已知空气质量评分值在区间（80，100]的5人中有2人被邀请参加座谈，求其中幸福指数评分值在区间（80，90]的仅有1人被邀请的概率．
