Question

【题目】已知函数，其中.

（1）讨论函数的单调性；

（2）若，记函数的两个极值点为，（其中），当的最大值为时，求实数的取值范围.

Answer 1

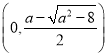【答案】(1) 当时,在上单调递增；当时,在和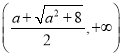上单调递增,在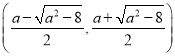上单调递减. (2)

【解析】

（1）先求得的导函数,并令.通过对判别式及的讨论,即可判断单调性.

（2）根据（1）可知当时,有两极值点,,且两个极值点为的两根.进而可得两个极值点间的关系.利用作差法可得的表达式,并令,及.进而通过求导得的单调性,进而根据最大值可求得的值.解得,的值.即可得的取值范围.

（1）.

令,则.

①当或,即时,得恒成立,

∴在上单调递增.

②当,即时,

由,得或；

由,得.

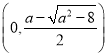∴函数在和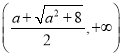上单调递增,

在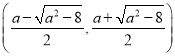上单调递减.

综上所述,当时,在上单调递增；

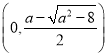当时,在和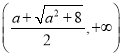上单调递增,

在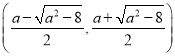上单调递减.

（2）由（1）得,当时,有两极值点,（其中）.

由（1）得,为的两根,

于是,.

∴

.

令,则.

∵,

∴在上单调递减.

由已知的最大值为,

而.

∴.

设的取值集合为,则只要满足且中的最小元素为2的集合均符合题意.

又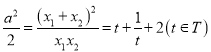,易知在上单调递增,

结合,可得与是一一对应关系.

而当,即时,联合,

解得,,进而可得.

∴实数的取值范围为.