题目内容
(08年黄冈中学一模文) (12分) 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a , ∠ABC=60°.平面ACEF⊥平面ABCD,且四边形ACEF是矩形,AF=a.
(I)求证:AC⊥BE;
(II)求二面角B-EF-D的余弦值.

解析:(I)∵AB∥CD,AD=DC=CB=a,∴四边形ABCD是等腰梯形.设AC交BD于N,连EN.
∵∠ABC=60°,∴∠DCB=∠ADC=120°,∠DAC=∠ACD=30°,
∴AC=![]() ,AB=2a,
,AB=2a,![]() =90°.
=90°.
又四边形ACEF是矩形,
∴AC⊥平面BCE.∴AC⊥BE.
(II)∵平面ACEF⊥平面ABCD, EC⊥AC,
∴EC⊥面 ABCD,∴EC⊥CD, EC⊥AD,又AF∥CE,
∴AF⊥AD,而AF=CE,AD=CD,
∴Rt△![]() ≌Rt△
≌Rt△![]() ,DE=DF.
,DE=DF.
过D作DG⊥EF于G,则G为EF的中点,于是EG=![]() .
.
在Rt△![]() 中,
中,![]()
![]() ,∴
,∴![]() .∴
.∴![]() .
.
设所求二面角大小为![]() ,则由
,则由![]() 及
及![]() ,
,![]() 得,
得,![]() ,
,
www.ks5u.com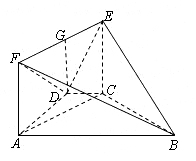

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目