题目内容
【题目】已知A,B是抛物线![]() 上的两点,且在x轴两侧,若AB的中点为Q,分别过A,B两点作T的切线,且两切线相交于点P.
上的两点,且在x轴两侧,若AB的中点为Q,分别过A,B两点作T的切线,且两切线相交于点P.
(1)求证:直线PQ平行于x轴;
(2)若直线AB经过抛物线T的焦点,求![]() 面积的最小值.
面积的最小值.
【答案】(1)证明见解析;(2)4
【解析】
(1)分别求出抛物线T在点![]() ,
,![]() 处切线的斜率,写出切线方程,将两切线方程联立解出点P的纵坐标,再求出点Q的纵坐标,即可判断直线PQ与x轴平行;
处切线的斜率,写出切线方程,将两切线方程联立解出点P的纵坐标,再求出点Q的纵坐标,即可判断直线PQ与x轴平行;
(2)把点P的纵坐标代入切线方程求出横坐标,得到点P的坐标,把直线AB的方程与抛物线的方程联立,利用韦达定理求出![]() ,
,![]() ,从而求出点P到直线AB的距离d以及
,从而求出点P到直线AB的距离d以及![]() ,再列出
,再列出![]() 面积的表达式,转化为求函数的最小值即可求解.
面积的表达式,转化为求函数的最小值即可求解.
解:由题意,不妨设A在第一象限,B在第四象限.
设![]() ,
,![]() .
.
(1)证明:抛物线![]() 在第一象限内的图象所对应的函数解析式为
在第一象限内的图象所对应的函数解析式为![]() 求导可得
求导可得![]() ,
,
所以过点A的切线的斜率![]() ,
,
所以直线AP的方程为![]() ,
,
把![]() 代入化简得
代入化简得![]() ,
,
同理可得直线BP的方程为![]() ,
,
联立方程消去x得![]() ,
,
即P点的纵坐标为![]() .
.
又因为Q点的纵坐标为![]() ,
,
所以直线PQ平行于x轴.
(2)设点P的坐标为![]() ,
,
由(1)知![]() ,
,
把![]() 代入直线BP的方程
代入直线BP的方程![]() ,
,
解得![]() ,所以
,所以![]() .
.
因为抛物线![]() 焦点的坐标为
焦点的坐标为![]() ,且直线AB的斜率不为零,
,且直线AB的斜率不为零,
所以设直线AB的方程为![]() ,
,
将直线AB的方程与抛物线的方程联立,
即![]() ,'消去x得
,'消去x得![]() ,
,
因为![]() ,
,
所以![]() ,
,![]() .
.
所以点P的坐标为![]() ,
,
设点P到直线AB的距离为d,
则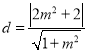 ,
,
又因为![]()
![]()
![]() ,
,
所以![]()
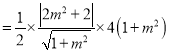
![]() .
.
故当![]() 时,
时,![]() 的面积取得最小值,最小值为4.
的面积取得最小值,最小值为4.

练习册系列答案
相关题目