题目内容
已知 是定义在R上的奇函数,当
是定义在R上的奇函数,当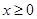 时
时 (m为常数),则
(m为常数),则 的值为( ).
的值为( ).
A. | B.6 | C.4 | D. |
D.
解析试题分析:因为 是定义在R上的奇函数,当
是定义在R上的奇函数,当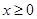 时
时 (m为常数),所以
(m为常数),所以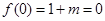 ,即
,即 ,即
,即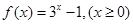 ;
; .
.
考点:函数的奇偶性、对数恒等式.

练习册系列答案
相关题目
已知定义在 上的函数
上的函数 是奇函数且满足
是奇函数且满足 ,
, ,数列
,数列 满足
满足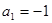 ,且
,且 ,(其中
,(其中 为
为 的前
的前 项和),则
项和),则 ( ).
( ).
A. | B. | C. | D. |
函数 =log2(3x-1)的定义域为( )
=log2(3x-1)的定义域为( )
| A.(0,+∞) | B.[0,+∞) | C.(1,+∞) | D.[1,+∞) |
已知函数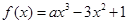 ,若
,若 存在唯一的零点
存在唯一的零点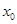 ,且
,且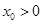 ,则
,则 的取值范围是( ).
的取值范围是( ).
A.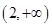 | B.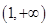 | C.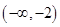 | D.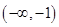 |
方程 实根的个数为( )
实根的个数为( )
| A.6 | B.5 | C.4 | D.3 |
下列式子中不能表示函数y=f(x)的是( ).
| A.x=y2+1 | B.y=2x2+1 |
| C.x-2y=6 | D.x= |
函数f(x)=lnx–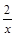 的零点所在的大致区间是( )
的零点所在的大致区间是( )
| A.(1, 2) | B.(2, 3) | C.(1,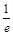 )和(3, 4) )和(3, 4) | D.(e, +∞) |
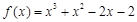 的一个正数零点附近的函数值用二分法计算,得数据如下:
的一个正数零点附近的函数值用二分法计算,得数据如下: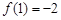
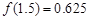
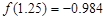
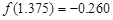

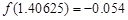
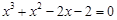 的一个最接近的近似根为( )
的一个最接近的近似根为( )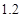 B.
B.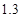 C.
C.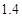 D.
D.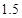
 且
且 ,设命题
,设命题 :函数
:函数 在R上单调递减,命题
在R上单调递减,命题 :不等式
:不等式 的解集为R,如果命题“
的解集为R,如果命题“ ”为真命题,“
”为真命题,“ ”为假命题,求实数
”为假命题,求实数 的取值范围
的取值范围