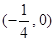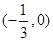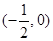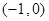题目内容
下列式子中不能表示函数y=f(x)的是( ).
| A.x=y2+1 | B.y=2x2+1 |
| C.x-2y=6 | D.x= |
A
解析试题分析:因为函数的概念包含两条:①非空数集A,B;②对于任意 ,都有唯一的
,都有唯一的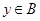 ;而选项A中,当
;而选项A中,当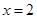 时,
时,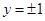 ,不满足函数的概念;故选A.
,不满足函数的概念;故选A.
考点:函数的概念.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知函数 ,定义如下:当
,定义如下:当 时,
时, ( ).
( ).
| A.有最大值1,无最小值 | B.有最小值0,无最大值 |
| C.有最小值—1,无最大值 | D.无最小值,也无最大值 |
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则 =( )
=( )
A.- | B.- | C. | D. |
已知 是定义在R上的奇函数,当
是定义在R上的奇函数,当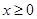 时
时 (m为常数),则
(m为常数),则 的值为( ).
的值为( ).
A. | B.6 | C.4 | D. |
若 是R上周期为5的奇函数,且满足
是R上周期为5的奇函数,且满足 ,则
,则 ( ).
( ).
A. | B. | C. | D. |
已知函数 ,若关于x的方程f(f(x))=0有且仅有一个实数解,则实数a的取值范围是( ).
,若关于x的方程f(f(x))=0有且仅有一个实数解,则实数a的取值范围是( ).
| A.(-∞,0) | B.(-∞,0)∪(0,1) |
| C.(0,1) | D.(0,1)∪(1,+∞) |
若函数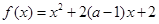 在区间
在区间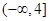 内递减,那么实数
内递减,那么实数 的取值范围为( )
的取值范围为( )
A.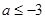 | B.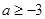 | C.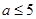 | D.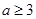 |
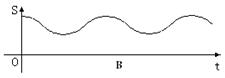
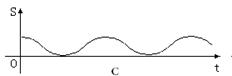
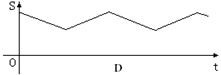
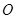 点沿三角形列的底边匀速向前滚动(如图),设滚动中的圆与系列正三角形的重叠部分(如图中的阴影)的面积
点沿三角形列的底边匀速向前滚动(如图),设滚动中的圆与系列正三角形的重叠部分(如图中的阴影)的面积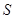 关于时间
关于时间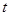 的函数为
的函数为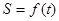 ,则下列图中与函数
,则下列图中与函数

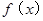 是以
是以 为周期的偶函数,当
为周期的偶函数,当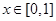 时,
时,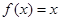 ,那么在区间
,那么在区间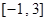 内,关于
内,关于 的方程
的方程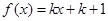 (
(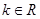 且
且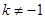 )有
)有 个不同的根,则
个不同的根,则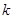 的取值范围是( )
的取值范围是( )