题目内容
函数
＝log2(3x－1)的定义域为( )
| A．(0，＋∞) | B．[0，＋∞) | C．(1，＋∞) | D．[1，＋∞) |
A
解析试题分析：由已知得：
，故选Ａ．
考点：函数的定义域．
练习册系列答案
相关题目
的定义域为R；
，对一切正实数均成立．定义域为R的函数
满足
，当
[0，2)时
若
时，
恒成立，则实数t的取值范围是( )
A．[-2，0) (0，l) | B．[-2，0)[l，+∞) |
| C．[-2，l] | D．( ，-2](0，l] |
设f(x)是周期为2的奇函数，当0≤x≤1时，f(x)＝2x(1－x)，则
＝( )
A．－ | B．－ | C． | D． |
下列函数中，满足“
”的单调递增函数是（ ）
A． | B． | C． | D． |
已知
是定义在R上的奇函数，当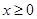
时
（m为常数）,则
的值为（ ）.
A． | B．6 | C．4 | D． |
已知函数
,若关于x的方程f(f(x))＝0有且仅有一个实数解，则实数a的取值范围是( ).
| A．(－∞，0) | B．(－∞，0)∪(0,1) |
| C．(0,1) | D．(0,1)∪(1，＋∞) |
下列函数中，在[1，＋∞)上为增函数的是( )．
| A．y＝(x－2)2 | B．y＝|x－1| | C．y＝ | D．y＝－(x＋1)2 |