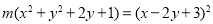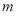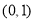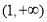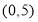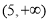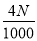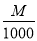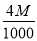题目内容
已知函数
(1)当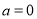 时,求
时,求 的最小值;
的最小值;
(2)在区间(1,2)内任取两个实数p,q,且p≠q,若不等式 >1恒成立,求实数a的取值范围;
>1恒成立,求实数a的取值范围;
(3)求证: (其中
(其中 )。
)。
(1)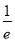 ;(2)
;(2)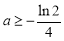 (3)详见解析
(3)详见解析
【解析】
试题分析:(1)求导,令导数大于0得增区间,令导数小于0得减区间,根据函数的单调性求其最小值。(2)因为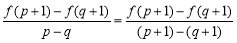 ,表示点
,表示点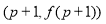 与点
与点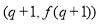 连成的斜率,可将问题转化为直线的斜率问题。根据导数的几何意义可求其斜率,将
连成的斜率,可将问题转化为直线的斜率问题。根据导数的几何意义可求其斜率,将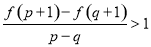 恒成立问题转化为求函数最值问题,求最值时还是用求导再求其单调性的方法求其最值。(3)由(2)可得
恒成立问题转化为求函数最值问题,求最值时还是用求导再求其单调性的方法求其最值。(3)由(2)可得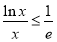 ,则有
,则有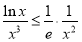 。用放缩法可证此不等式。
。用放缩法可证此不等式。
试题解析:【解析】
(1)
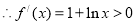 得
得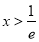
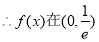 上递减,
上递减,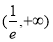 上递增。
上递增。
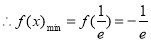 。 4分
。 4分
(2)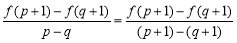 ,
,
表示点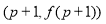 与点
与点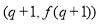 连成的斜率,又
连成的斜率,又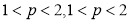 ,
,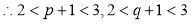 ,即函数图象在区间(2,3)任意两点连线的斜率大于1,
,即函数图象在区间(2,3)任意两点连线的斜率大于1,
即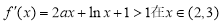 内恒成立. 6分
内恒成立. 6分
所以,当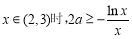 恒成立.
恒成立.
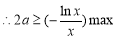
设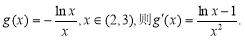
若
当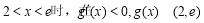 上单调递减;
上单调递减;
当 上单调递增. 9分
上单调递增. 9分
又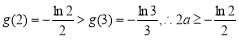
故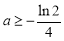 10分
10分
(3)由(2)得,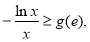

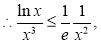 11分
11分
所以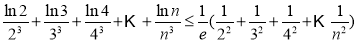
又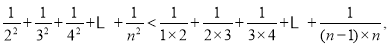
而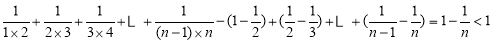
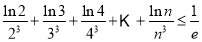 成立. 14分
成立. 14分
考点:用导数研究函数的性质。

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目