Question

【题目】（本题满分12分）已知椭圆C： 的离心率为， 是椭圆的两个焦点， 是椭圆上任意一点，且的周长是．

（1）求椭圆C的方程；

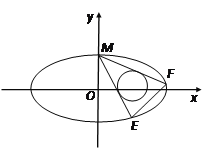
（2）设圆T： ，过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点，当圆心在轴上移动且时，求EF的斜率的取值范围．

Answer 1

【答案】（1）；（2）.

【解析】试题分析：（1）由椭圆离心率得到a，c的关系，再由△PF1F2的周长是8+2得a，c的另一关系，联立求得a，c的值，代入隐含条件求得b，则椭圆方程可求；（2）椭圆的上顶点为M（0，1），设过点M与圆T相切的直线方程为y=kx+1，由圆心到切线距离等于半径得到关于切线斜率的方程，由根与系数关系得到

，再联立一切线方程和椭圆方程，求得E的坐标，同理求得F坐标，另一两点求斜率公式得到．然后由函数单调性求得EF的斜率的范围

试题解析：（1）由，即，可知a=4b， ，

∵△PF1F2的周长是，

∴，∴a=4，b=1，所求椭圆方程为；

（2）椭圆的上顶点为M（0，1），设过点M与圆T相切的直线方程为y=kx+1，

由直线y=kx+1与T相切可知，

即（9t2﹣4）k2+18tk+5=0，

∴，

由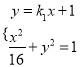，得．

∴， 同理，

则．

当1＜t＜3时， 为增函数，故EF的斜率的范围为．