题目内容
 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为PC的中点,AD=CD.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为PC的中点,AD=CD.(1)证明PA∥平面BDE;
(2)证明AC⊥平面PBD.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)设AC∩BD=H,连结EH.只要证明EH∥PA.
(2)由(1)可得,DB⊥AC.因为PD⊥平面ABCD,AC?平面ABCD,所以PD⊥AC.根据线面垂直的判定定理可证.
(2)由(1)可得,DB⊥AC.因为PD⊥平面ABCD,AC?平面ABCD,所以PD⊥AC.根据线面垂直的判定定理可证.
解答:
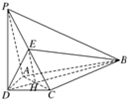 证明:(1)设AC∩BD=H,
证明:(1)设AC∩BD=H,
连结EH.在△ADC中,因为AD=CD,且DB平分
∠ADC,所以H为AC的中点.
又由题设,E为PC的中点,故EH∥PA.
又EH?平面BDE且PA?平面BDE,
所以PA∥平面BDE.
证明:(2)因为PD⊥平面ABCD,AC?平面ABCD,
所以PD⊥AC.
由(1)可得,DB⊥AC.
又PD∩DB=D,
故AC⊥平面PBD.
 证明:(1)设AC∩BD=H,
证明:(1)设AC∩BD=H,连结EH.在△ADC中,因为AD=CD,且DB平分
∠ADC,所以H为AC的中点.
又由题设,E为PC的中点,故EH∥PA.
又EH?平面BDE且PA?平面BDE,
所以PA∥平面BDE.
证明:(2)因为PD⊥平面ABCD,AC?平面ABCD,
所以PD⊥AC.
由(1)可得,DB⊥AC.
又PD∩DB=D,
故AC⊥平面PBD.
点评:本题考查了线面平行的判定定理和线面垂直的判定定理的运用,关键是熟练判定定理的体积,正确运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=(
sinx-cosx)cosx的值域是( )
| 3 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
已知(0,-4)是椭圆3kx2+ky2=1的一个焦点,则实数k的值是( )
| A、6 | ||
B、
| ||
| C、24 | ||
D、
|