题目内容
3.在公比为2的等比数列{an}中,a2+1是a1与a3的等差中项.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)记数列{an}前n项的和为Sn,若数列{bn}满足bn=anlog2(Sn+2),试求数列{bn}前n项的和Tn.
分析 (I)由a2+1是a1与a2的等差中项,可得2(a2+1)=a1+a3,解得a1=2.利用等比数列的通项公式即可得出an.
(II)由Sn=$\frac{2({2}^{n}-1)}{2-1}$,可得bn=(n+1)•2n,再利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 解:(I)∵a2+1是a1与a2的等差中项,
∴2(a2+1)=a1+a3,
∴2(2a1+1)=a1+4a1,解得a1=2.
∴an=2n.
(II)Sn=$\frac{2({2}^{n}-1)}{2-1}$=2n+1-2,
∴bn=anlog2(Sn+2)=(n+1)•2n,
∴Tn=2×2+3×22+…+(n+1)×2n,
2Tn=2×22+3×23+…+n×2n+(n+1)×2n+1,
∴-Tn=4+22+23+…+2n-(n+1)×2n+1=2+$\frac{2({2}^{n}-1)}{2-1}$-(n+1)×2n+1=-n•2n+1,
∴Tn=n•2n+1.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.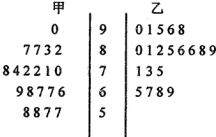 为了研究“教学方式”对教学质量的影响,某校数学老师分别用两种不同的教学方式对入学时数学平均分数和优秀率都相同的甲、乙两个班级进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
为了研究“教学方式”对教学质量的影响,某校数学老师分别用两种不同的教学方式对入学时数学平均分数和优秀率都相同的甲、乙两个班级进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学中至少有一名被抽中的概率:
(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断是否有99%把握认为“成绩优秀与教学方式有关”.
下面临界值表仅供参考:
参考公式:x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$.
 为了研究“教学方式”对教学质量的影响,某校数学老师分别用两种不同的教学方式对入学时数学平均分数和优秀率都相同的甲、乙两个班级进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
为了研究“教学方式”对教学质量的影响,某校数学老师分别用两种不同的教学方式对入学时数学平均分数和优秀率都相同的甲、乙两个班级进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学中至少有一名被抽中的概率:
(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断是否有99%把握认为“成绩优秀与教学方式有关”.
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.79 | 10.828 |
8.一个组合体的主视图和左视图相同,如图,其体积为22π,则图中的x为( )


| A. | 4 | B. | 4.5 | C. | 5 | D. | 5.5 |
7.函数f(x)=2sinx+tanx+m,$x∈[-\frac{π}{3},\frac{π}{3}]$有零点,则m的取值范围是( )
| A. | $[2\sqrt{3},+∞)$ | B. | $(-∞,2\sqrt{3}]$ | C. | (-∞,2$\sqrt{3}$)∪(2$\sqrt{3}$,+∞) | D. | $[-2\sqrt{3},2\sqrt{3}]$ |
 如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=$\frac{1}{2}$AB=1,点M在线段EC上.
如图,边长为$\sqrt{2}$的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=$\frac{1}{2}$AB=1,点M在线段EC上. 函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中,A,C为图象与x轴的两个交点,B为图象的最低点,P为图象与y轴的交点.若在曲线段$\widehat{ABC}$与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为$\frac{π}{4}$.
函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中,A,C为图象与x轴的两个交点,B为图象的最低点,P为图象与y轴的交点.若在曲线段$\widehat{ABC}$与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为$\frac{π}{4}$.