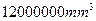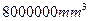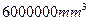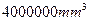题目内容
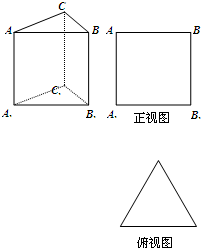
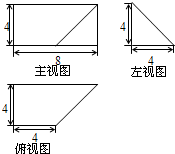
如图所示是一几何体的三视图，则该几何体外接球的表面积为（ ）
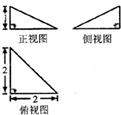
| A．3π | B．4π | C．8π | D．9π |
由三视图可知：该几何体是一个三棱锥，高为1，底面是腰长为2的等腰直角三角形．
如图所示，建立空间直角坐标系．取线段AB的中点，则DA=DB=DC．设球心为O，则OD⊥平面ABC．
∵D（1，1，0），∴可设球心O（1，1，z），又B（0，2，0），P（0，0，1）．
∵|OB|=|OP|=R（球的半径）．
∴
=
，解得z=
．
∴R=
=
．
∴该几何体外接球的表面积S=4π×(
)2=9π．
故选D．
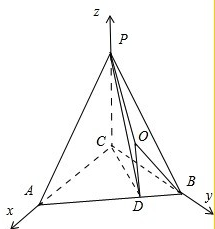
如图所示，建立空间直角坐标系．取线段AB的中点，则DA=DB=DC．设球心为O，则OD⊥平面ABC．
∵D（1，1，0），∴可设球心O（1，1，z），又B（0，2，0），P（0，0，1）．
∵|OB|=|OP|=R（球的半径）．
∴
| 1+1+z2 |
| 1+1+(z-1)2 |
| 1 |
| 2 |
∴R=
1+1+(
|
| 3 |
| 2 |
∴该几何体外接球的表面积S=4π×(
| 3 |
| 2 |
故选D．
练习册系列答案
相关题目
），可得这个几何体的体积是（ ）
