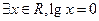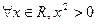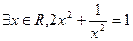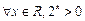题目内容
(本小题满分12分)已知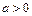 ,设命题p:函数
,设命题p:函数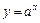 在R上单调递减,q:设函数
在R上单调递减,q:设函数 ,函数
,函数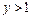 恒成立,若
恒成立,若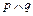 为假,
为假,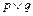 为真,求a的取值范围.
为真,求a的取值范围.
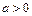 ,设命题p:函数
,设命题p:函数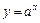 在R上单调递减,q:设函数
在R上单调递减,q:设函数 ,函数
,函数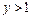 恒成立,若
恒成立,若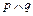 为假,
为假,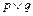 为真,求a的取值范围.
为真,求a的取值范围.a的取值范围为0<a≤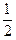 或a≥1
或a≥1
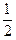 或a≥1
或a≥1解:若p是真命题,则0<a<1………………………………………………2分
若q是真命题,即ymin>1,又ymin="2a " ∴2a>1,
∴ q为真命题时a>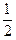 ;………………………………………………………………6分
;………………………………………………………………6分
又∵p∨q为真,p∧q为假,∴p与q一真一假.………………………………………8分
若p真q假,则0<a≤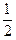 ;若p假q真,则a≥1.…………………………………10分
;若p假q真,则a≥1.…………………………………10分
故a的取值范围为0<a≤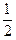 或a≥1………………………………………………12分
或a≥1………………………………………………12分
若q是真命题,即ymin>1,又ymin="2a " ∴2a>1,
∴ q为真命题时a>
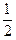 ;………………………………………………………………6分
;………………………………………………………………6分又∵p∨q为真,p∧q为假,∴p与q一真一假.………………………………………8分
若p真q假,则0<a≤
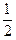 ;若p假q真,则a≥1.…………………………………10分
;若p假q真,则a≥1.…………………………………10分故a的取值范围为0<a≤
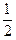 或a≥1………………………………………………12分
或a≥1………………………………………………12分
练习册系列答案
相关题目
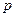 :关于
:关于 的函数
的函数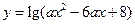 的定义域是
的定义域是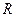 ;命题
;命题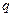 :当
:当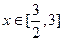 时,
时,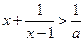 恒成立. 如果命题“
恒成立. 如果命题“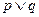 ”是真命题,“
”是真命题,“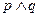 ”是假命题,求实数
”是假命题,求实数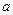 的取值范围.
的取值范围.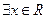 ,
,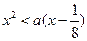 ;命题
;命题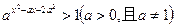 的解集为
的解集为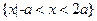 ;命题Q:
;命题Q: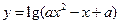 的定义域为R.如果P或Q为真,P且Q为假,求
的定义域为R.如果P或Q为真,P且Q为假,求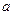 的取值范
的取值范 围.
围.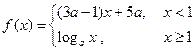 ,现给出下列命题:
,现给出下列命题: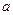 =
=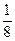 ;
;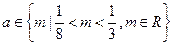 时,不等式
时,不等式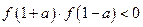 恒成立;
恒成立;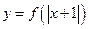 是偶函数 . 其中正确的命题是 ( )
是偶函数 . 其中正确的命题是 ( )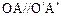 ,
,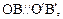 则
则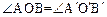 ;②直角梯形是平面图形;③
;②直角梯形是平面图形;③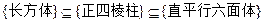 ; ④若
; ④若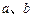 是两条异面直线,
是两条异面直线,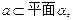
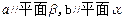 ,则
,则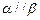 ;⑤在四面体
;⑤在四面体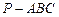 中,
中,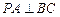 ,
,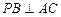 ,则点
,则点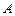 在面
在面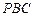 内的射影为
内的射影为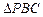 的垂心,其中真命题的个数是( )
的垂心,其中真命题的个数是( )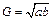 是
是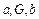 成等比数列的充分不必要条件;
成等比数列的充分不必要条件;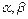 满足
满足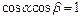 ,则
,则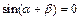 ;
;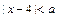 的解集非空,则必有
的解集非空,则必有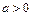 ;
;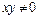 ”是指 “
”是指 “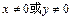 ”
”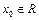 ,
,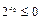 ”的否定是“对任意的
”的否定是“对任意的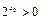 ”.
”.  (把你认为正确的命题的序号都填上).
(把你认为正确的命题的序号都填上). 
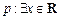 ,
,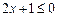 ,则命题
,则命题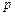 的否定是( )
的否定是( )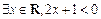
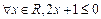
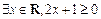
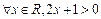
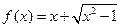 是非奇非偶函数
是非奇非偶函数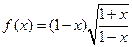 是偶函数
是偶函数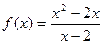 是奇函数
是奇函数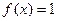 既是奇函数又是偶函数
既是奇函数又是偶函数