题目内容
如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?
广告的高为140 cm,宽为175 cm时,可使广告的面积最小
解析试题分析:解法1:设矩形栏目的高为a cm,宽为b cm,则ab=9000. ①
广告的高为a+20,宽为2b+25,其中a>0,b>0.
广告的面积S=(a+20)(2b+25)
=2ab+40b+25a+500=18500+25a+40b
≥18500+2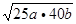 =18500+
=18500+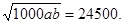
当且仅当25a=40b时等号成立,此时b=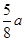 ,代入①式得a=120,从而b=75.
,代入①式得a=120,从而b=75.
即当a=120,b=75时,S取得最小值24500.
故广告的高为140 cm,宽为175 cm时,可使广告的面积最小.
解法2:设广告的高为宽分别为x cm,y cm,则每栏的高和宽分别为x-20,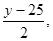 其中x>20,y>25
其中x>20,y>25
两栏面积之和为2(x-20)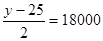 ,由此得y=
,由此得y=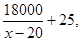
广告的面积S=xy=x(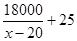 )=
)=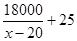 x,
x,
整理得S=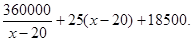
因为x-20>0,所以S≥2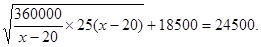
当且仅当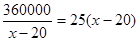 时等号成立,
时等号成立,
此时有(x-20)2=14400(x>20),解得x=140,代入y=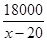 +25,得y=175,
+25,得y=175,
即当x=140,y=175时,S取得最小值24500,
故当广告的高为140 cm,宽为175 cm时,可使广告的面积最小.
考点:不等式求解最值
点评:解决的关键是利用函数的性质或者是均值不等式求解最值,关键是设好变量,表示广告的面积,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
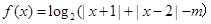 .
.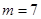 时,求函数
时,求函数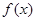 的定义域;
的定义域; 的不等式
的不等式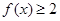 的解集是
的解集是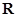 ,求
,求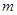 的取值范围.
的取值范围.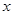 (元/件),可近似看做一次函数
(元/件),可近似看做一次函数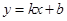 的关系(图象如下图所示).
的关系(图象如下图所示).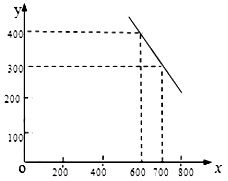
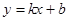 的表达式;
的表达式;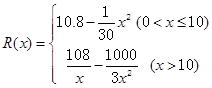
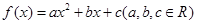 满足下列条件:
满足下列条件: 时,
时,  的最小值为0,且
的最小值为0,且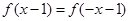 恒成立;
恒成立; 时,
时,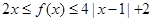 恒成立.
恒成立.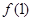 的值;
的值;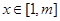 时,就有
时,就有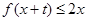 成立
成立 (2)
(2)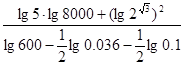
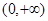 的函数
的函数 ,对任意的
,对任意的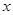 、
、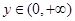 ,都有
,都有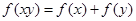 ,且当
,且当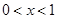 时,
时,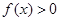 .
.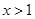 时,
时,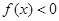 ;
;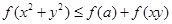 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.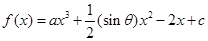 的图象过点
的图象过点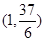 ,且在
,且在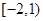 内单调递减,在
内单调递减,在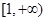 上单调递增。
上单调递增。 的解析式;
的解析式;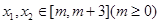 ,不等式
,不等式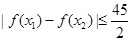 恒成立,试问这样的
恒成立,试问这样的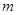 是否存在.若存在,请求出
是否存在.若存在,请求出 (1)求函数
(1)求函数 的定义域;
的定义域;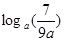 ,求实数
,求实数 的值。
的值。