题目内容
已知定义在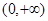 的函数
的函数 ,对任意的
,对任意的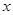 、
、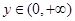 ,都有
,都有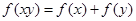 ,且当
,且当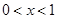 时,
时,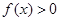 .
.
(1)证明:当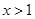 时,
时,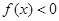 ;
;
(2)判断函数 的单调性并加以证明;
的单调性并加以证明;
(3)如果对任意的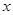 、
、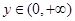 ,
,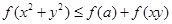 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)先证明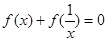 ,进而证明当
,进而证明当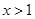 时,
时,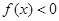 ;
;
(2)严格按照单调函数的定义证明即可;
(3)
解析试题分析:(1)证明:取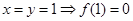 ,
,
又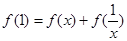 ,即
,即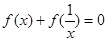 ,
,
所以当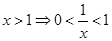 时,
时,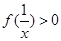 ;
;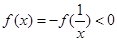 .
.
(2) 在
在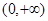 上是减函数,证明如下:
上是减函数,证明如下:
设 ,
,
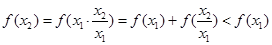
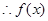 在
在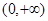 上是减函数.
上是减函数.
(3)  ,
,
而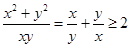 ,所以实数
,所以实数 的取值范围为
的取值范围为 .
.
考点:本小题主要考查抽象函数的性质.
点评:解决抽象函数问题的主要方法是“赋值法”,而且抽象函数的单调性的证明知能用定义,利
用基本不等式求最值时,要注意“一正二定三相等”三个条件缺一不可.

练习册系列答案
相关题目


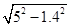 -0.8=4,
-0.8=4,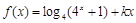
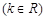 是偶函数.
是偶函数.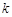 的值;
的值;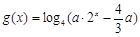 ,若函数
,若函数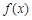 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围.
的取值范围.
 的图象关于
的图象关于 轴对称,且在区间
轴对称,且在区间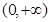 上是减函数,
上是减函数, 的解析式;((2)若
的解析式;((2)若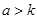 ,比较
,比较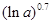 与
与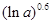 的大小;
的大小; ,当
,当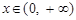 时,有
时,有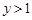 ,解关于x的不等式
,解关于x的不等式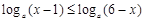
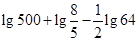
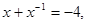 求
求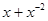 的值。
的值。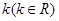 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点. 的图象关于原点对称。
的图象关于原点对称。 在
在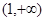 上的单调性,并根据定义证明。
上的单调性,并根据定义证明。