题目内容
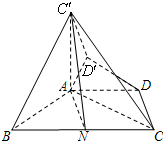 (2013•门头沟区一模)在等腰梯形ABCD中,AD∥BC,AD=
(2013•门头沟区一模)在等腰梯形ABCD中,AD∥BC,AD=| 1 | 2 |
(Ⅰ)求证:AC⊥平面ABC′;
(Ⅱ)求证:C′N∥平面ADD′;
(Ⅲ)求二面角A-C′N-C的余弦值.
分析:(Ⅰ)由梯形的性质和N是BC的中点可得四边形ANCD是平行四边形,得到AN=DC;利用等腰梯形可得AN=AB,又∠ABC=60°,得到△ABN是等边三角形,于是AN=BN=NC,由出可得△ABC是直角三角形,即AC⊥AB,再利用面面垂直的性质即可得到结论;
(Ⅱ)由已知可得:AD∥BC,AD′∥BC′,利用面面平行的判定定理即可得出;
(Ⅲ)如图所示的空间直角坐标系,求出两个平面的法向量,利用法向量的夹角即可得到二面角的一余弦值.
(Ⅱ)由已知可得:AD∥BC,AD′∥BC′,利用面面平行的判定定理即可得出;
(Ⅲ)如图所示的空间直角坐标系,求出两个平面的法向量,利用法向量的夹角即可得到二面角的一余弦值.
解答:(Ⅰ)证明:∵AD=
BC,N是BC的中点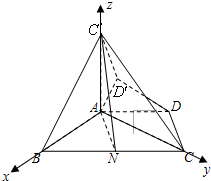 ,
,
∴AD=NC,又AD∥BC,
∴四边形ANCD是平行四边形,∴AN=DC.
又∵等腰梯形,∴AN=AB.
又∠ABC=60°,
∴△ABN是等边三角形.
∴AN=BN=
BC,
∴△ABC是直角三角形,且∠BAC=90°.
∴AC⊥AB.
∵平面C′BA⊥平面ABC,
∴AC⊥平面ABC′.
(Ⅱ)证明:∵AD∥BC,AD′∥BC′,
AD′∩AD=A,BC∩BC′=B,
∴平面ADD′∥平面BCC′,
∴C′N∥平面ADD′.
(Ⅲ)∵AC⊥平面ABC′,
同理AC′⊥平面ABC,建立如图如示坐标系
设AB=1,
则B(1,0,0),C(0,
,0),C′(0,0,
),N(
,
,0),
则
=(-1,0,
),
=(0,-
,
).
设平面C′NC的法向量为
=(x,y,z),
则
,即
,
令z=1,则x=
,y=1,得
=(
,1,1).
∵AC′⊥平面ABC,∴平面C′AN⊥平面ABC.
又BD⊥AN,平面C′AN∩平面ABC=AN,
∴BD⊥平面C′AN,
设BD与AN交于点O,O则为AN的中点,O(
,
,0).
所以平面C′AN的法向量
=(
,-
,0).
∴cosθ=
=
.
由图形可知二面角A-C′N-C为钝角.
所以二面角A-C′N-C的余弦值为-
.
| 1 |
| 2 |
 ,
,∴AD=NC,又AD∥BC,
∴四边形ANCD是平行四边形,∴AN=DC.
又∵等腰梯形,∴AN=AB.
又∠ABC=60°,
∴△ABN是等边三角形.
∴AN=BN=
| 1 |
| 2 |
∴△ABC是直角三角形,且∠BAC=90°.
∴AC⊥AB.
∵平面C′BA⊥平面ABC,
∴AC⊥平面ABC′.
(Ⅱ)证明:∵AD∥BC,AD′∥BC′,
AD′∩AD=A,BC∩BC′=B,
∴平面ADD′∥平面BCC′,
∴C′N∥平面ADD′.
(Ⅲ)∵AC⊥平面ABC′,
同理AC′⊥平面ABC,建立如图如示坐标系
设AB=1,
则B(1,0,0),C(0,
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
则
| BC′ |
| 3 |
| CC′ |
| 3 |
| 3 |
设平面C′NC的法向量为
| n |
则
|
|
令z=1,则x=
| 3 |
| n |
| 3 |
∵AC′⊥平面ABC,∴平面C′AN⊥平面ABC.
又BD⊥AN,平面C′AN∩平面ABC=AN,
∴BD⊥平面C′AN,
设BD与AN交于点O,O则为AN的中点,O(
| 1 |
| 4 |
| ||
| 4 |
所以平面C′AN的法向量
| OB |
| 3 |
| 4 |
| ||
| 4 |
∴cosθ=
| ||||
|
|
| ||
| 5 |
由图形可知二面角A-C′N-C为钝角.
所以二面角A-C′N-C的余弦值为-
| ||
| 5 |
点评:熟练掌握等腰梯形的性质、平行四边形的判定与性质、等边三角形及直角三角形的判定与性质、面面垂直与平行的判定及性质、通过建立空间直角坐标系利用法向量的夹角求空间角是解题的关键.

练习册系列答案
相关题目
 (2013•门头沟区一模)如图已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.
(2013•门头沟区一模)如图已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.