题目内容
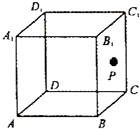
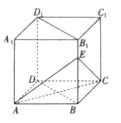
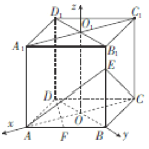
【题目】如图,在各棱长均为4的直四棱柱![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() 为棱
为棱![]() 上一点,且
上一点,且![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由底面![]() 为菱形,可得
为菱形,可得![]() ,根据直棱柱的性质可得
,根据直棱柱的性质可得![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,从而根据面面垂直的判定定理可得平面
,从而根据面面垂直的判定定理可得平面![]() 平面
平面![]() ;(2)设
;(2)设![]() 与
与![]() 交于点
交于点![]() ,
, ![]() 与
与![]() 交于点
交于点![]() ,以
,以![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,分别根据向量垂直数量积为零列方程组求出平面
,分别根据向量垂直数量积为零列方程组求出平面![]() 与平面
与平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得二面角
的一个法向量,根据空间向量夹角余弦公式,可得二面角![]() 的余弦值.
的余弦值.
试题解析:(1)证明:∵底面![]() 为菱形,∴
为菱形,∴![]() .
.
在直四棱柱![]() 中,∴
中,∴![]() 底面
底面![]() , ∴
, ∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)解:设![]() 与
与![]() 交于点
交于点![]() ,
, ![]() 与
与![]() 交于点
交于点![]() ,以
,以![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,如图所示,则
,如图所示,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
,
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则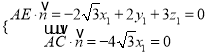 ,
,
取![]() ,则
,则![]() .
.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
易证![]() 平面
平面![]() ,从而平面
,从而平面![]() 的一个法向量为
的一个法向量为![]() .
.
∴ ,
,
∴由图可知,二面角![]() 为锐角,二面角
为锐角,二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查面面垂直的证明以及利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.

【题目】若学生![]() 一天学习数学超过两个小时的概率为
一天学习数学超过两个小时的概率为![]() (每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(Ⅰ)①设学生![]() 本周一天学习数学超过两个小时的天数为
本周一天学习数学超过两个小时的天数为![]() 求
求![]() 的分布列与数学期望
的分布列与数学期望![]()
②求学生![]() 本周数学学习投入的概率.
本周数学学习投入的概率.
(Ⅱ)为了研究学生学习数学的投入程度和本周数学周练成绩的关系,随机在年级中抽取了![]() 名学生进行调查,所得数据如下表所示:
名学生进行调查,所得数据如下表所示:
成绩理想 | 成绩不太理想 | 合计 | |
数学学习投入 | 20 | 10 | 30 |
数学学习不太投入 | 10 | 15 | 25 |
合计 | 30 | 25 | 55 |
根据上述数据能否有![]() 的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
附:![]()
|
|
|
|
|
|
|
|
|
|
| 10.828 |