题目内容
已知数列{an}的前n项和为Sn,a1=-
,
+Sn-1=-2(n≥2,n∈N*).
(1)求S1,S2,S3,S4的值;
(2)猜想Sn的表达式;并用数学归纳法加以证明.
| 1 |
| 2 |
| 1 |
| Sn |
(1)求S1,S2,S3,S4的值;
(2)猜想Sn的表达式;并用数学归纳法加以证明.
(1)∵数列{an}的前n项和为Sn,a1=-
,
+Sn-1=-2(n≥2,n∈N*),
∴S1=-
,S2=-
,S3=-
,S4=-
.…(4分)(每个1分)
(2)猜想Sn=-
(n∈N*),…(6分)
数学归纳法证明:(1)当n=1时,S1=a1=-
,猜想成立;….(7分)
(2)假设n=k(k≥2,k∈N* )时猜想成立,即有:Sk=-
,
则n=k+1时,因为
=-Sk-2…(8分)
∴
=
-2=-
;…(10分)
从而有Sk+1=-
,即n=k+1时,猜想也成立;
由(1)(2)可知,Sn=-
(n∈N*),成立…(12分)
| 1 |
| 2 |
| 1 |
| Sn |
∴S1=-
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
(2)猜想Sn=-
| n |
| n+1 |
数学归纳法证明:(1)当n=1时,S1=a1=-
| 1 |
| 2 |
(2)假设n=k(k≥2,k∈N* )时猜想成立,即有:Sk=-
| k |
| k+1 |
则n=k+1时,因为
| 1 |
| Sk+1 |
∴
| 1 |
| Sk+1 |
| k |
| k+1 |
| k+2 |
| k+1 |
从而有Sk+1=-
| k+1 |
| k+2 |
由(1)(2)可知,Sn=-
| n |
| n+1 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,求证
,求证
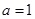 ”是“复数
”是“复数 (
( ,i为虚数单位)是纯虚数”的( )
,i为虚数单位)是纯虚数”的( )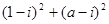 是纯虚数,则实数
是纯虚数,则实数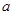 等于( )
等于( )



 没有最小数”时,可用反证法证明.
没有最小数”时,可用反证法证明. 是
是 中的最小数,则取
中的最小数,则取 ,可得:
,可得: ,与假设中“
,与假设中“ 是
是 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设 是
是 中的最大数,则可以找到
中的最大数,则可以找到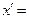 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知 ,
, ,这与假设矛盾!所以数集
,这与假设矛盾!所以数集