题目内容
【题目】已知数列{an}中,a1=1,a2n=n﹣an , a2n+1=an+1,则a1+a2+a3+…+a100= .
【答案】1306
【解析】解:∵a2n=n﹣an , a2n+1=an+1, ∴an=n﹣a2n , an=a2n+1﹣1,∴a2n+1+a2n=n+1,
∴a1+(a2+a3)+(a4+a5)+…+(a98+a99)=1+2+3+…+50=1275,
a100=50﹣a50=50﹣(25﹣a25)
=25+a12+1
=26+(6﹣a6)=32﹣(3﹣a3)
=29+(a1+1)
=31,
∴a1+a2+a3+…+a100=1275+31=1306.
所以答案是:1306.
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系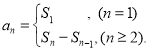 .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
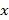
(1)试问这3年的前7个月中哪个月的月平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: 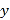 ,
, ![]() .
.
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);

(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?

