题目内容
【题目】平面α过正方体ABCD﹣A1B1C1D1的面对角线 
，且平面α⊥平面C1BD，平面α∩平面ADD1A1=AS，则∠A1AS的正切值为（ ）
A.
B.
C.
D.
【答案】D
【解析】解：正方体ABCD﹣A1B1C1D1中，BD⊥AC，BD⊥AA1 ， ∵AC∩AA1=A，∴BD⊥平面AA1C，∴A1C⊥BD，
同理，得A1C⊥BC1 ，
∵BD∩BC1=B，∴A1C⊥平面C1BD，
如图，以AA1为侧棱补作一个正方体AEFG﹣A1PQS，
使得侧面AGRA1与平面ADD1A1共面，
连结AQ，则AQ∥CA1 ， 连结QB1 ， 交A1R于S，则平面AQB1就是平面α，且AS为所求作，
∵AQ∥CA1 ， ∴AQ⊥平面C1BD，
∵AQ平面α，∴平面α⊥平面C1BD，
∴tan∠A1AS= 
= 
．
故选：D．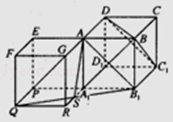
【考点精析】认真审题，首先需要了解平面与平面垂直的性质(两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直)．
练习册系列答案
相关题目
