题目内容
【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )
①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行.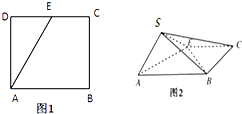
A.0
B.1
C.2
D.3
【答案】B
【解析】解:①当直线SA⊥平面SBC时,BC平面SBC,∴SA⊥BC;
又AD∥BC,则SA⊥AD,这与∠SAD为锐角矛盾,∴①错误;②∵平面SBC∩直线SA=S,
∴平面SBC内的直线与SA相交或异面,②错误;③过点C作CF∥AE,交AB于F,∵CF平面SAE,AE平面SAE,
由线面平行的判定定理得,CF∥平面SAE,∴③正确;
综上,正确的命题是③.
所以答案是:B.
【考点精析】解答此题的关键在于理解平面与平面垂直的性质的相关知识,掌握两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.

练习册系列答案
相关题目
【题目】某种商品价格与该商品日需求量之间的几组对照数据如表:
价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?
参考公式:线性回归方程 ![]() ,其中
,其中 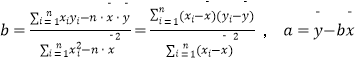 .
.