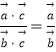Question

【题目】在△ABC中，内角A，B，C所对应的边分别为a，b，c，若c（acosB﹣ b）=a2﹣b2 ．
（1）求角A；
（2）若a= ，求c﹣b的取值范围．

Answer 1

【答案】
（1）解：由 ， ，

得a2+c2﹣b2﹣bc=2a2﹣2b2，

∴a2=b2+c2﹣bc，

∵a2=b2+c2﹣2bccosA，

∴ ，

∵角A为三角形内角，

∴ ；

（2）解：∵ ，

∴b=2sinB，c=2sinC，

∴ ，

∵ ，

∴ ，

∴ ，

∴c﹣b∈（﹣1，1）．

【解析】1、由已知根据余弦定理可得cosA的值，即得 A。
2、利用正弦定理可求出cb=2sinc2sin，根据三角形内角和为，利用诱导公式转化为sin(A+B)2sinB，再利用两角和差的正弦公式转化为
2 s i n ( B ) ，根据已知角的取值范围可得 s i n ( B )的取值范围即得c﹣b的值。