题目内容
已知f(x)=2x- x2,g(x)=logax(a>0且a≠1),h(x)=f(x)-g(x)在定义域上为减函数,且其导函数h′(x)存在零点.
x2,g(x)=logax(a>0且a≠1),h(x)=f(x)-g(x)在定义域上为减函数,且其导函数h′(x)存在零点.
(I)求实数a的值;
(II)函数y=p(x)的图象与函数y=g(x)的图象关于直线y=x对称,且y=p′(x)为函数y=p(x)的导函数,A(x1,y1),B(x2,y2),(x1<x2)是函数y=p(x)图象上两点,若p′(x0)= ,判断P(x0),,P(x1),P(x2)的大小,并证明你的结论.
,判断P(x0),,P(x1),P(x2)的大小,并证明你的结论.
解:(I)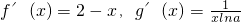
∵h(x)=f(x)-g(x)在定义域上为减函数
∴h′(x)≤0在(0,+∞)上恒成立即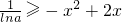 在(0,+∞)上恒成立
在(0,+∞)上恒成立
即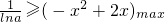 x∈(0,+∞)
x∈(0,+∞)
令u(x)=-x2+2x=-(x-1)2+1≤1
∴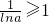
∵h′(x)存在零点
∴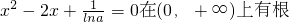
∴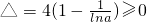
∴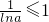
∴lna=1即a=e
(II)∵g(x)=lnx,p(x)=ex
令F(x)=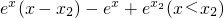
F′(x)=ex+exx-x2ex-ex=(x-x2)ex<0
∴F(x)在(-∞,x2)上递减
∴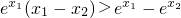
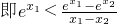
同理
所以有P(x1)<P(x0)<P(x2)
分析:(I)令h′(x)≤0在(0,+∞)上恒成立,分离出 ,求出二次函数(-x2+2x)max,令
,求出二次函数(-x2+2x)max,令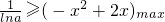 求出a的范围.
求出a的范围.
(II)通过分析法,构造函F((x),通过导数判断出F(x)的单调性,判断出P(x0),P(x1),P(x2)的大小.
点评:解决不等式恒成立,常采用的方法是分离参数,构造新函数,转化为求函数的最值.
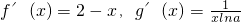
∵h(x)=f(x)-g(x)在定义域上为减函数
∴h′(x)≤0在(0,+∞)上恒成立即
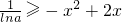 在(0,+∞)上恒成立
在(0,+∞)上恒成立即
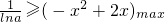 x∈(0,+∞)
x∈(0,+∞)令u(x)=-x2+2x=-(x-1)2+1≤1
∴
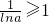
∵h′(x)存在零点
∴
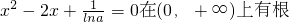
∴
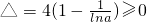
∴
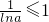
∴lna=1即a=e
(II)∵g(x)=lnx,p(x)=ex
令F(x)=
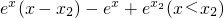
F′(x)=ex+exx-x2ex-ex=(x-x2)ex<0
∴F(x)在(-∞,x2)上递减
∴
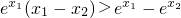
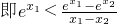
同理

所以有P(x1)<P(x0)<P(x2)
分析:(I)令h′(x)≤0在(0,+∞)上恒成立,分离出
 ,求出二次函数(-x2+2x)max,令
,求出二次函数(-x2+2x)max,令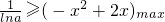 求出a的范围.
求出a的范围.(II)通过分析法,构造函F((x),通过导数判断出F(x)的单调性,判断出P(x0),P(x1),P(x2)的大小.
点评:解决不等式恒成立,常采用的方法是分离参数,构造新函数,转化为求函数的最值.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目