题目内容
(2013•大连一模)选修4-5:不等式选讲
已知f(x)=|2x-1|+ax-5(a是常数,a∈R)
(Ⅰ)当a=1时求不等式f(x)≥0的解集.
(Ⅱ)如果函数y=f(x)恰有两个不同的零点,求a的取值范围.
已知f(x)=|2x-1|+ax-5(a是常数,a∈R)
(Ⅰ)当a=1时求不等式f(x)≥0的解集.
(Ⅱ)如果函数y=f(x)恰有两个不同的零点,求a的取值范围.
分析:(Ⅰ)当a=1时转化不等式f(x)≥0,去掉绝对值,然后求解不等式的解集即可.
(Ⅱ)函数y=f(x)恰有两个不同的零点,构造函数利用函数的图象推出a的取值范围.
(Ⅱ)函数y=f(x)恰有两个不同的零点,构造函数利用函数的图象推出a的取值范围.
解答: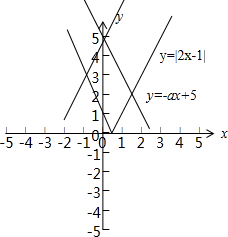 解:(Ⅰ)f(x)=|2x-1|+x-5=
解:(Ⅰ)f(x)=|2x-1|+x-5=
,
∴f(x)=|2x-1|+x-5≥0:化为
或
,
解得:{x|x≥2或x≤-4}.(5分)
(Ⅱ)由f(x)=0得,|2x-1|=-ax+5.(7分)
令y=|2x-1|,y=-ax+5,作出它们的图象,可以知道,当-2<a<2时,
这两个函数的图象有两个不同的交点,
所以,函数y=f(x)有两个不同的零点.(10分)
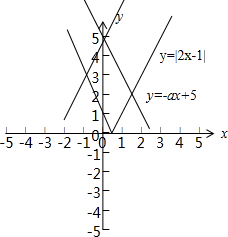 解:(Ⅰ)f(x)=|2x-1|+x-5=
解:(Ⅰ)f(x)=|2x-1|+x-5=
|
∴f(x)=|2x-1|+x-5≥0:化为
|
|
解得:{x|x≥2或x≤-4}.(5分)
(Ⅱ)由f(x)=0得,|2x-1|=-ax+5.(7分)
令y=|2x-1|,y=-ax+5,作出它们的图象,可以知道,当-2<a<2时,
这两个函数的图象有两个不同的交点,
所以,函数y=f(x)有两个不同的零点.(10分)
点评:本题考查绝对值不等式的解法,函数的零点定理的应用,考查计算能力.

练习册系列答案
相关题目
 (2013•大连一模)定义在R上的函数f(x)满足f(3)=1,f(-2)=3,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,且f′(x)有且只有一个零点,若非负实数a,b满足f(2a+b)≤1,f(-a-2b)≤3,则
(2013•大连一模)定义在R上的函数f(x)满足f(3)=1,f(-2)=3,f′(x)为f(x)的导函数,已知y=f′(x)的图象如图所示,且f′(x)有且只有一个零点,若非负实数a,b满足f(2a+b)≤1,f(-a-2b)≤3,则