题目内容
【题目】如图在四棱锥![]() 中,平面
中,平面![]() 底面ABCD,底面ABCD是等腰梯形,
底面ABCD,底面ABCD是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.
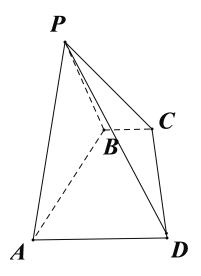
(1)证明:![]() .
.
(2)求平面PCD与平面PAB夹角(锐角)的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)过P作PO⊥AB与O.连OC,OD,根据已知条件计算可得![]() ,根据平面与平面垂直的性质定理可得
,根据平面与平面垂直的性质定理可得![]() ,再根据直线与平面垂直的判定和性质可证结论
,再根据直线与平面垂直的判定和性质可证结论
(2)以O为坐标原点.OD,OB,OP为x,y,![]() 轴建立空间直角坐标洗,利用空间向量可求得平面PCD与平面PAB夹角(锐角)的余弦值.
轴建立空间直角坐标洗,利用空间向量可求得平面PCD与平面PAB夹角(锐角)的余弦值.
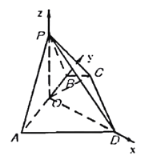
(1)证明:过P作PO⊥AB与O.连OC,OD,如图:

因为底面ABCD是等腰梯形,![]() ,
,
所以![]() ,因为
,因为![]() ,
,![]() ,
,
∴![]() ,所以
,所以![]() ,
,
所以![]() ,
,
∴![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
因为平面![]() 底面ABCD,交线为AB,
底面ABCD,交线为AB,
∴![]() 底面ABCD,所以
底面ABCD,所以![]() .
.
又![]() ,
,![]() 平面POC,
平面POC,
故![]() 平面POC,所以
平面POC,所以![]() ;
;
(2)由(1)知![]() ,以O为坐标原点.OD,OB,OP为x,y,
,以O为坐标原点.OD,OB,OP为x,y,![]() 轴建立空间直角坐标系,如图所示
轴建立空间直角坐标系,如图所示
则![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
设平面PCD的法向量![]() ,
,
故 ,即
,即 ,
,
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
平面PAB的法向量取![]() ),
),
所以![]()
故平面PCD与PAB夹角的余弦值为![]() .
.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目