题目内容
(2013•顺义区二模)设定义在R上的函数f(x)是最小正周期为2π的偶函数,f′(x)是f(x)的导函数.当x∈[0,π]时,0<f(x)<1;当x∈(0,π)且x≠
时,(x-
)f′(x)<0.则函数y=f(x)-cosx在[-3π,3π]上的零点个数为
| π |
| 2 |
| π |
| 2 |
6
6
.分析:根据x∈[0,π]时,0<f(x)<1;当x∈(0,π)且x≠
时,(x-
)f′(x)<0,确定函数的单调性,再利用函数的图形,即可得到结论.
| π |
| 2 |
| π |
| 2 |
解答:解:∵x∈(0,π) 且x≠
时,(x-
)f′(x)<0
∴x∈(0,
),函数单调增,x∈(
,π),函数单调减.
∵x∈[0,π]时,0<f(x)<1,
在R上的函数f(x)是最小正周期为2π的偶函数,在同一坐标系中作出y=cosx和y=f(x)草图如下,
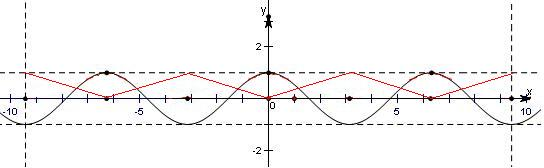
由图知y=f(x)-cosx在[-3π,3π]上的零点个数为6个.
故答案为:6.
| π |
| 2 |
| π |
| 2 |
∴x∈(0,
| π |
| 2 |
| π |
| 2 |
∵x∈[0,π]时,0<f(x)<1,
在R上的函数f(x)是最小正周期为2π的偶函数,在同一坐标系中作出y=cosx和y=f(x)草图如下,

由图知y=f(x)-cosx在[-3π,3π]上的零点个数为6个.
故答案为:6.
点评:本题考查函数的单调性,考查函数的零点,考查函数的周期性与奇偶性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目