题目内容
7.已知函数f(x)=ax-$\frac{a}{x}$-2lnx(a>0),g(x)=$\frac{2a}{x}$(1)求f(x)的单调区间;
(2)若对区间[1,e]上任意x1和x2总有f(x1)<g(x2),求实数a取值范围.
分析 (1)求导,利用二次函数判断导函数正负,确定原函数单调区间
(2)求区间[1,e]上,两函数的最值,f(x)max<g(x)min,需要对a进行分类讨论.
解答 解:(1)f′(x)=$\frac{a{x}^{2}-2x+a}{{x}^{2}}$,
令h(x)=ax2-2x+a,
△=4-4a2.
当△≤0即a≥1时,h(x)≥0恒成立,
f(x)在定义域内递增;
当△>0即0<a<1时,
当在(0,$\frac{1-\sqrt{1-{a}^{2}}}{a}$)和($\frac{1+\sqrt{1-{a}^{2}}}{a}$,+∞)时,
h(x)>0,f(x)递增;
当在($\frac{1-\sqrt{1-{a}^{2}}}{a}$,$\frac{1+\sqrt{1-{a}^{2}}}{a}$)时,
h(x)<0,f(x)递减.
(2)当a≥1时,
f(x)max=ae-$\frac{a}{e}$-2,g(x)min=$\frac{2a}{e}$,
∴ae-$\frac{a}{e}$-2<$\frac{2a}{e}$,
∴a<$\frac{2e}{{e}^{2}-3}$,
故1≤a<$\frac{2e}{{e}^{2}-3}$;
当0<a<1时,
f(1)=0,
f(e)=ae-$\frac{a}{e}$-2,
当e≤$\frac{1-\sqrt{1-{a}^{2}}}{a}$即a≥$\frac{2e}{1+{e}^{2}}$,
f(x)max=ae-$\frac{a}{e}$-2,
∴ae-$\frac{a}{e}$-2<$\frac{2a}{e}$,
∴a<$\frac{2e}{{e}^{2}-3}$,
∴1>a≥$\frac{2e}{1+{e}^{2}}$;
当1≥$\frac{1-\sqrt{1-{a}^{2}}}{a}$且e≤$\frac{1+\sqrt{1-{a}^{2}}}{a}$即a<$\frac{1}{e}$,
f(x)max=f(0)=0<$\frac{2a}{e}$恒成立,
∴0<a<$\frac{1}{e}$;
当e>$\frac{1+\sqrt{1-{a}^{2}}}{a}$即a>$\frac{2e}{1+{e}^{2}}$,
f(x)max=ae-$\frac{a}{e}$-2,
∴ae-$\frac{a}{e}$-2<$\frac{2a}{e}$,
∴a<$\frac{2e}{{e}^{2}-3}$,
∴1>a>$\frac{2e}{1+{e}^{2}}$.
故a的范围为1>a≥$\frac{2e}{1+{e}^{2}}$或0<a<$\frac{1}{e}$.
点评 考察了导数的应用和恒成立问题以及对参数的分类讨论问题

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案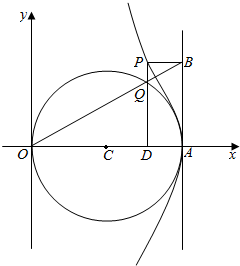 如图所示,OA是圆C的直径,且OA=2a,射线OB与圆交于Q点,和经过A点的切线交于B点,作PQ⊥OA交OA于D,PB∥OA,试求点P的轨迹的参数方程.
如图所示,OA是圆C的直径,且OA=2a,射线OB与圆交于Q点,和经过A点的切线交于B点,作PQ⊥OA交OA于D,PB∥OA,试求点P的轨迹的参数方程.