题目内容
12．已知B村位于A村的正西方1km处，原计划经过B村沿北偏东60°的方向设一条地下管线m，但在A村的西北方现400m处，发现一古代文物遗址w．根据初步侦探的结果，文物管理部门将遗址w周围100m范围划为禁区，试问埋设地下管线m的计划是否需要修改？分析 利用正弦定理求出AC，再求出A到直线BC的距离，即可得出结论．
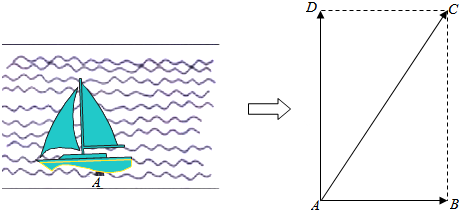
解答 
解：如图所示，△ABC中，AB=1km，∠CBA=30°，∠CAB=45°，
∴∠ACB=105°，
由正弦定理可得$\frac{1}{sin105°}=\frac{AC}{sin30°}$，
∴AC=$\frac{\sqrt{6}-\sqrt{2}}{2}$＞0.5，
又建立坐标系，可得直线BC的方程为y=$\frac{\sqrt{3}}{3}$x，A（1，0）到直线的距离为$\frac{\frac{\sqrt{3}}{3}}{\sqrt{\frac{1}{3}+1}}$=0.5
∴埋设地下管线m的计划不需要修改．
点评 本题考查了正弦定理，考查点到直线的距离公式，考查学生的计算能力，属于中档题．
练习册系列答案
走进文言文系列答案
相关题目
10．下列各组函数相等的是（ ）
| A． | f（x）=x-2，g（x）=$\frac{{x}^{2}-4}{x+2}$ | B． | f（x）=$\frac{|x|}{x}$，g（x）=1（x≠0） | ||
| C． | f（x）=x2-2x-1，g（t）=t2-2t-1 | D． | f（x）=$\frac{1}{2}$，g（x）=$\frac{（x-1）^{0}}{2}$ |
