题目内容
16.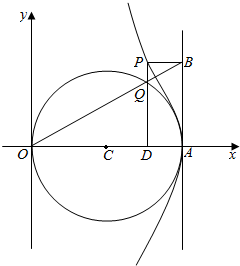 如图所示,OA是圆C的直径,且OA=2a,射线OB与圆交于Q点,和经过A点的切线交于B点,作PQ⊥OA交OA于D,PB∥OA,试求点P的轨迹的参数方程.
如图所示,OA是圆C的直径,且OA=2a,射线OB与圆交于Q点,和经过A点的切线交于B点,作PQ⊥OA交OA于D,PB∥OA,试求点P的轨迹的参数方程.
分析 首先,引入参数,取∠DOQ=θ,然后,分别表示点P的横坐标和纵坐标即可得到参数方程.
解答 解:设P(x,y)是轨迹上任意一点.取∠DOQ=θ.
∵PQ⊥OA交OA于D,PB∥OA,
∴x=OD=OQcosθ=OAcos2θ=2acos2θ.
y=AB=OAtanθ=2atanθ,
故P点的参数方程为$\left\{\begin{array}{l}{x=2aco{s}^{2}θ}\\{y=2atanθ}\end{array}\right.$,(θ为参数,且-$\frac{π}{2}<θ<\frac{π}{2}$).
点评 本题重点考查了参数方程的求解方法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
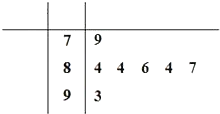 某校举行2010年元旦汇演,如图是7位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数是85,方差为1.6.
某校举行2010年元旦汇演,如图是7位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数是85,方差为1.6.