题目内容
【题目】已知椭圆![]() 的两焦点与短轴的一个端点的连线构成面积为
的两焦点与短轴的一个端点的连线构成面积为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆E的标准方程;
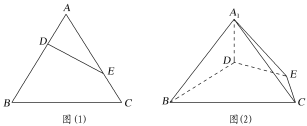
(2)直线![]() 与椭圆交于点A、B,线段
与椭圆交于点A、B,线段![]() 的中点为M,射线MO与椭圆交于点P,点O为
的中点为M,射线MO与椭圆交于点P,点O为![]() 的重心,试问:
的重心,试问:![]() 的面积S是否为定值,若是,求出这个值;若不是,求S的取值范围.
的面积S是否为定值,若是,求出这个值;若不是,求S的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 的面积
的面积![]() 为定值
为定值![]() .
.
【解析】
(1)依题意可得: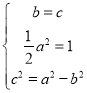 ,解得
,解得![]() ,可得椭圆
,可得椭圆![]() 的方程.
的方程.
(2)若直线![]() 的斜率不存在,由已知可得
的斜率不存在,由已知可得![]() ,
,![]() ,可求得
,可求得![]() 的面积S;若直线
的面积S;若直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() ,直线与椭圆的方程联立可得
,直线与椭圆的方程联立可得![]() ,则
,则![]() ,
,![]() ,
,![]() ,由点
,由点![]() 为
为![]() 的重心,设
的重心,设![]() ,求得点P的坐标,代入椭圆的方程中得到m与k的关系
,求得点P的坐标,代入椭圆的方程中得到m与k的关系![]() ,再运用三角形的面积公式求得
,再运用三角形的面积公式求得![]() 的面积,得出结论.
的面积,得出结论.
(1)依题意得: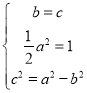 ,解得
,解得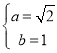 ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.

(2)若直线![]() 的斜率不存在,因为点O为
的斜率不存在,因为点O为![]() 的重心,所以
的重心,所以![]() ,
,![]() ,
,
所以![]() 的面积
的面积![]() .
.
若直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() ,
,
即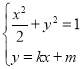 ,联立化简得
,联立化简得![]() ,
,
则![]() ,
,![]() ,
,![]()
由题意点![]() 为
为![]() 的重心,设
的重心,设![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,![]() ,代入椭圆
,代入椭圆![]() ,
,
得![]() ,整理得
,整理得![]() ,
,
设坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]() 的面积
的面积
![]()
![]()
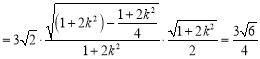 .
.
综上可得![]() 的面积
的面积![]() 为定值
为定值![]() .
.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案【题目】某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评,同时也为公司赢得丰厚的利润.该公司![]() 年至
年至![]() 年的年利润
年的年利润![]() 关于年份代号
关于年份代号![]() 的统计数据如下表(已知该公司的年利润与年份代号线性相关).
的统计数据如下表(已知该公司的年利润与年份代号线性相关).
年份 |
|
|
|
|
|
|
|
年份代号 |
|
|
|
|
|
|
|
年利润 |
|
|
|
|
|
|
|
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程,并预测该公司
的线性回归方程,并预测该公司![]() 年(年份代号记为
年(年份代号记为![]() )的年利润;
)的年利润;
(Ⅱ)当统计表中某年年利润的实际值大于由(Ⅰ)中线性回归方程计算出该年利润的估计值时,称该年为![]() 级利润年,否则称为
级利润年,否则称为![]() 级利润年.将(Ⅰ)中预测的该公司
级利润年.将(Ⅰ)中预测的该公司![]() 年的年利润视作该年利润的实际值,现从
年的年利润视作该年利润的实际值,现从![]() 年至
年至![]() 年这
年这![]() 年中随机抽取
年中随机抽取![]() 年,求恰有
年,求恰有![]() 年为
年为![]() 级利润年的概率.
级利润年的概率.
参考公式: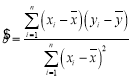 ,
,![]() .
.
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在A,B实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在A,B试验地随机抽选各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.

(1)求图中a的值,并求综合评分的中位数;
(2)用样本估计总体,以频率作为概率,若在A,B两块实验地随机抽取3棵花苗,求所抽取的花苗中的优质花苗数的分布列和数学期望;
(3)填写下面的列联表,并判断是否有90%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ,其中
,其中![]() .)
.)
【题目】某校为确定数学成绩与玩手机之间的关系,从全校随机抽样调查了40名同学,其中40%的人玩手机.这40位同学的数学分数(百分制)的茎叶图如图①所示.数学成绩不低于70分为良好,低于70分为一般.
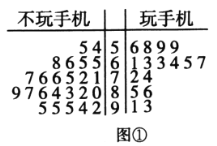
(1)根据以上资料完成下面的![]() 列联表,并判断有多大把握认为“数学成绩良好与不玩手机有关系”.
列联表,并判断有多大把握认为“数学成绩良好与不玩手机有关系”.
数学成绩良好 | 数学成绩一般 | 总计 | |
不玩手机 | |||
玩手机 | |||
总计 | 40 |
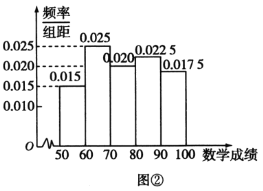
(2)现将40名同学的数学成绩分为如下5组:
![]() ,其频率分布直方图如图②所示.计算这40名同学数学成绩的平均数,由茎叶图得到的真实值记为
,其频率分布直方图如图②所示.计算这40名同学数学成绩的平均数,由茎叶图得到的真实值记为![]() ,由频率分布直方图得到的估计值记为
,由频率分布直方图得到的估计值记为![]() (同一组中的数据用该组区间的中点值作代表),求
(同一组中的数据用该组区间的中点值作代表),求![]() 与
与![]() 的误差值.
的误差值.
(3)从这40名同学数学成绩高于90分的7人中随机选取2人,求至少有一人玩手机的概率.
附:![]() ,
,
这40名同学的数学成绩总和为2998分.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |