题目内容
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在A,B实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在A,B试验地随机抽选各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图.记综合评分为80及以上的花苗为优质花苗.

(1)求图中a的值,并求综合评分的中位数;
(2)用样本估计总体,以频率作为概率,若在A,B两块实验地随机抽取3棵花苗,求所抽取的花苗中的优质花苗数的分布列和数学期望;
(3)填写下面的列联表,并判断是否有90%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ,其中
,其中![]() .)
.)
【答案】(1)![]() ,82.5;(2)分布列见解析,
,82.5;(2)分布列见解析,![]() ;(3)列联表见解析,有90%的把握认为优质花苗与培育方法有关系.
;(3)列联表见解析,有90%的把握认为优质花苗与培育方法有关系.
【解析】
(1)根据各段的频率之和为1,可得![]() ,然后假设中位数,并根据在中位数的左右两边的频率均为
,然后假设中位数,并根据在中位数的左右两边的频率均为![]() ,简单计算,可得结果.
,简单计算,可得结果.
(2)假设所抽取的花苗为优质花苗的颗数为X,可知![]() ,然后计算相对应颗数的概率,画出分布列,最后根据期望的计算公式,可得结果.
,然后计算相对应颗数的概率,画出分布列,最后根据期望的计算公式,可得结果.
(3)先计算出优质花苗的频率,然后可得优质花苗的颗数,进一步得出其他的数据,最后计算![]() ,根据表格进行比较,可得结果.
,根据表格进行比较,可得结果.
(1)由![]() ,
,
解得![]() .
.
令得分中位数为x,由![]() ,
,
解得![]() .
.
故综合评分的中位数为82.5.
(2)由(1)与频率分布直方图 ,
优质花苗的频率为![]() ,即概率为
,即概率为![]() ,
,
设所抽取的花苗为优质花苗的颗数为X,则![]() ,
,
 ;
;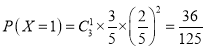 ;
;
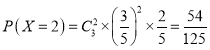 ;
; .
.
其分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以,所抽取的花苗为优质花苗的数学期望![]() .
.
(3)结合(1)与频率分布直方图,
优质花苗的频率为![]() ,
,
则样本中,优质花苗的颗数为60棵,列联表如下表所示:
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | 30 | 50 |
乙培育法 | 40 | 10 | 50 |
合计 | 60 | 40 | 100 |
可得![]() .
.
所以,有90%的把握认为优质花苗与培育方法有关系.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】癌症是迄今为止人类尚未攻克的疾病之一,目前,癌症只能尽量预防.某医学中心推出了一种抗癌症的制剂,现对20位癌症病人,进行医学试验测试药效,测试结果分为“病人死亡”和“病人存活”,现对测试结果和药物剂量(单位:![]() )进行统计,规定病人在服用
)进行统计,规定病人在服用![]() (包括
(包括![]() )以上为“足量”,否则为“不足量”,统计结果显示,这20病人
)以上为“足量”,否则为“不足量”,统计结果显示,这20病人
中“病人存活”的有13位,对病人服用的药物剂量统计如下表:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
吸收量/ | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 10 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
已知“病人存活”,但服用的药物剂量不足的病人共1位.
(1)完成下列![]() 列联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为“病人存活”与服用药物的剂量足量有关?
列联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为“病人存活”与服用药物的剂量足量有关?
服用药物足量 | 服用药物不足量 | 合计 | |
病人存活 | 1 | ||
病人死亡 | |||
合计 | 20 |
(2)若在该样本“服用药物剂量不足”的病人中随机抽取3位,求这三人中恰有1位“病人存活”的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()