题目内容
已知数列{an}的通项公式为
，其中a、b、c均为正数，那么an________an+1（填＞、＜、=之一）
＜
分析：由，（a，b，c∈（0，+∞），知=
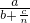，由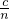
随着n的增大而减小，知an＜an+1．
解答：∵，（a，b，c∈（0，+∞）
∴=，
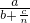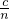∵随着n的增大而减小，
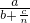∴随着n的增大而增大，
∴{an}是递增数列，
故an＜an+1，
故答案为：＜．
点评：本题考查数列的性质和应用，是基础题．解题时要认真审题，仔细解答，注意数列的单调性的应用．
分析：由
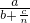，（a，b，c∈（0，+∞），知=，由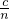随着n的增大而减小，知an＜an+1．解答：∵
，（a，b，c∈（0，+∞）∴
=，∵
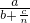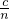随着n的增大而减小，∴
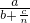随着n的增大而增大，∴{an}是递增数列，
故an＜an+1，
故答案为：＜．
点评：本题考查数列的性质和应用，是基础题．解题时要认真审题，仔细解答，注意数列的单调性的应用．
练习册系列答案
相关题目
已知数列{an}的通项为an=2n-1，Sn为数列{an}的前n项和，令bn=
，则数列{bn}的前n项和的取值范围为（ ）
| 1 |
| Sn+n |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、[
|