题目内容

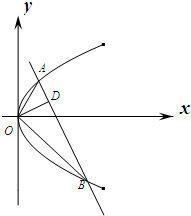
如图：已知直线与抛物线y2=2px（p＞0）交于A，B两点，且OA⊥OB，OD⊥AB交AB于点D，点D的坐标为（2，1）．
（1）求p的值；
（2）求△AOB的面积．
解（1）∵OD⊥AB，∴kOD•kAB=-1．
又kOD=
1
2
，∴kAB=-2，
∴直线AB的方程为y=-2x+5．…．…（1分）
设A（x1，x2），B（x2，y2），则
由OA⊥OB⇒
OA
•
OB
=0⇒x1x2+y1y2=0…．…（2分）
又x1x2+y1y2=x1x2+（-2x1+5）（-2x2+5）=5x1x2-10（x1+x2）+25
联立方程
y2=2px
y=-2x+5
消y可得4x2-（20+2p）x+25=0①
∴x1+x2=
10+p
2
，x1x2=
25
4
…．（3分）
∴x1x2+y1y2=5×
25
4
-10×
10+p
2
+25=
5
4
-p，
∴p=
5
4

当p=
5
4
时，方程①成为8x2-45x+50=0显然此方程有解．
∴p=
5
4
…．…（5分）
（2）由|AB|=
(1+k2)[(x1+x2)2-4x1x2]
=
5×[(
15
8
)2-25]
=
5
85
8
．…（7分）
∵|OD|=
5
．…（8分）
∴S△AOB=
1
2
|AB|•|OD|=
1
2
×
5
×
5
85
8
=
25
17
16
…．…（10分）
练习册系列答案
相关题目
在平面直角坐标系中，已知
a
=(2mx，y-1)，
b
=(2x，y+1)，其中m∈R，
a
⊥
b
，动点M（x，y）的轨迹为C．
（1）求轨迹C的方程，并说明该轨迹方程所表示曲线的形状；
（2）当m=
1
8
时，设过定点P（0，2）的直线l与轨迹C交于不同的两点A、B，且∠AOB为锐角（其中O为坐标原点），求直线l的斜率k的取值范围．
点P在直线l：y=x-1上，若存在过P的直线交抛物线y=x2于A，B两点，且
PA
=
AB
，则称点P为“λ点”，那么直线l上有______个“λ点”．
抛物线C：y2=2px（p＞0）的焦点为F，抛物线C上点M的横坐标为2，且|MF|=3．
（1）求抛物线C的方程；
（2）过焦点F作两条相互垂直的直线，分别与抛物线C交于M、N和P、Q四点，求四边形MPNQ面积的最小值．
如图所示，F1、F2分别为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点（1，
3
2
）到F1、F2两点的距离之和为4．
（1）求椭圆C的方程和焦点坐标；
（2）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求弦长|PQ|．
已知椭圆C1的方程为
x2
4
+y2=1，双曲线C2的左、右焦点分别为C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点．
（Ⅰ）求双曲线C2的方程；
（Ⅱ）若直线l：y=kx+
2
与椭圆C1及双曲线C2都恒有两个不同的交点，且l与C2的两个交点A和B满足
OA
•
OB
＜6（其中O为原点），求k的取值范围．
若θ是任意实数，则方程x2+4y2sinθ=1所表示的曲线一定不是（　　）
A．圆B．双曲线C．直线D．抛物线
直线L：y=kx+1与椭圆C：ax2+y2=2（a＞1）交于A、B两点，以OA、OB为邻边作平行四边形OAPB（O为坐标原点）．
（1）若k=1，且四边形OAPB为矩形，求a的值；
（2）若a=2，当k变化时（k∈R），求点P的轨迹方程．
如图，在以点O为圆心，AB为直径的半圆中，D为半圆弧的中心，P为半圆弧上一点，且AB=4，∠POB=30°，双曲线C以A，B为焦点且经过点P．
（1）建立适当的平面直角坐标系，求双曲线C的方程；
（2）设过点D的直线l与双曲线C相交于不同两点E、F，若△OEF的面积不小于2
2
，求直线l的斜率的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网