题目内容
【题目】已知在平面直角坐标系中,![]() ,
,![]() (
(![]() ),其中数列
),其中数列![]() 、
、![]() 都是递增数列.
都是递增数列.
(1)若![]() ,
,![]() ,判断直线
,判断直线![]() 与
与![]() 是否平行;
是否平行;
(2)若数列![]() 、
、![]() 都是正项等差数列,它们的公差分别为
都是正项等差数列,它们的公差分别为![]() 、
、![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() (
(![]() ),求证:
),求证:![]() 也是等差数列;
也是等差数列;
(3)若![]() ,
,![]() (
(![]() ),
),![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,数列
,数列![]() 前8项依次递减,求满足条件的数列
前8项依次递减,求满足条件的数列![]() 的个数.
的个数.
【答案】(1)不平行;(2)证明见解析;(3)9个.
【解析】
(1)确定A1(3,0),B1(0,4),A2(5,0),B2(0,7),求得斜率,可得A1B1与A2B2不平行;
(2)因为{an},{bn}为等差数列,设它们的公差分别为d1和d2,则an=a1+(n﹣1)d1,bn=b1+(n﹣1)d2,an+1=a1+nd1,bn+1=b1+nd2,从而可得![]() ,进而可证明数列{Sn}是等差数列;
,进而可证明数列{Sn}是等差数列;
(3)求得![]() ,根据数列{kn}前8项依次递减,可得an﹣a+b<0对1≤n≤7(n∈Z)成立,根据数列{bn}是递增数列,故只要n=7时,7a﹣a+b=6a+b<0即可,关键b1=a+b≥﹣12,联立不等式
,根据数列{kn}前8项依次递减,可得an﹣a+b<0对1≤n≤7(n∈Z)成立,根据数列{bn}是递增数列,故只要n=7时,7a﹣a+b=6a+b<0即可,关键b1=a+b≥﹣12,联立不等式 作出可行域,即可得到结论.
作出可行域,即可得到结论.
(1)由题意A1(3,0),B1(0,4),A2(5,0),B2(0,7),
所以![]() ,
,
![]() ,
,
因为![]() ,所以A1B1与A2B2不平行.
,所以A1B1与A2B2不平行.
(2)因为{an},{bn}为等差数列,设它们的公差分别为d1和d2,
则an=a1+(n﹣1)d1,bn=b1+(n﹣1)d2,an+1=a1+nd1,bn+1=b1+nd2
由题意![]()
所以![]() [b1+(n﹣1)d2]}
[b1+(n﹣1)d2]}
![]() ,
,
所以![]() ,
,
所以Sn+1﹣Sn=d1d2是与n无关的常数,
所以数列{Sn}是等差数列
(3)因为An(an,0),Bn(0,bn),
所以![]()
又数列{kn}前8项依次递减,
所以![]() 0,
0,
对1≤n≤7(n∈Z)成立,
即an﹣a+b<0对1≤n≤7(n∈Z)成立.
又数列{bn}是递增数列,所以a>0,故只要n=7时,7a﹣a+b=6a+b<0即可.
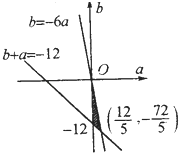
又b1=a+b≥﹣12,联立不等式 作出可行域(如右图所示),易得a=1或2,
作出可行域(如右图所示),易得a=1或2,
当a=1时,﹣13≤b<﹣6即b=﹣13,﹣12,﹣11,﹣10,﹣9,﹣8,﹣7,有7个解;
当a=2时,﹣14≤b<﹣12,即b=﹣14,﹣13,有2个解,所以数列{bn}共有9个.

 名题金卷系列答案
名题金卷系列答案【题目】2019年某地遭遇严重干旱,某乡计划向上级申请支援,为上报需水量,乡长事先抽样调查100户村民的月均用水量,得到这100户村民月均用水量(单位:t)的频率分布表如下:
月均用水量分组 | 频数 | 频率 |
| 12 | |
| ||
| 40 | |
| 0.18 | |
| 6 | |
合计 | 100 | 1.00 |
(1)请完成该频率分布表,并画出相对应的频率分布直方图.
(2)样本的中位数是多少?
(3)已知上级将按每户月均用水量向该乡调水,若该乡共有1200户,请估计上级支援该乡的月调水量是多少吨.

