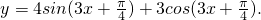题目内容
求下列函数的周期:(1)f(x)=sinx+cosx;
(2)f(x)=cos2x+2![]() sinxcosx-sin2x.
sinxcosx-sin2x.
解析:(1)f(x)=sinx+cosx=![]() sin(x+
sin(x+![]() ),
),
∴函数f(x)的周期为2π.
(2)f(x)=cos2x+2![]() sinxcosx-sin2x=
sinxcosx-sin2x=![]() sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+![]() ),
),
∴函数f(x)的周期为π.
点评:求一般三角函数周期的主要方法是公式法,即先化为y=Asin(ωx+φ)或y=Acos(ωx+φ)的形式,再用公式求出周期,形如y=asinx+bcosx,y=asin2x+bsinxcosx+ccos2x的函数都可化为y=Asin(ωx+φ)的形式,其次可以用定义法或图象观察法.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
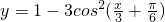 ;
;