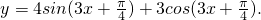题目内容
求下列函数的周期:(1)y=sin2x;(2)y=3cos![]() ;(3)y=2sin(2x-
;(3)y=2sin(2x-![]() ).
).
思路分析:本题主要考查y=Asin(ωx+φ).y=Acos(ωx+φ)的周期的求法.利用周期函数定义及诱导公式求函数的周期.
解:(1)由于f(x+π)=sin2(x+π)=sin(2x+2π)=sin2x=f(x),所以由周期函数的定义知,原函数的周期为π.
(2)由于f(x+4π)=3cos[12(x+4π)]=3cos(![]() +2π)=3cos
+2π)=3cos![]() =f(x),所以,由周期函数的定义知,原函数的周期为4π.
=f(x),所以,由周期函数的定义知,原函数的周期为4π.
(3)由于f(x+π)=2sin[2(x+π)-![]() ]=2sin[2x+2π-
]=2sin[2x+2π-![]() ]=2sin(2x-
]=2sin(2x-![]() )=f(x),由周期函数的定义知,原函数的周期为π.
)=f(x),由周期函数的定义知,原函数的周期为π.
温馨提示
由上例可以看到函数的周期仅与x的系数有关.一般地,y=Asin(ωx+φ)或y=Acos(ωx+φ)(其中A、ω、φ为常数,A≠0,ω>0)的周期T=2πω,若y=f(x)的周期为T,则y=f(ωx)的周期为![]() .
.

练习册系列答案
相关题目
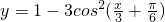 ;
;