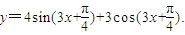题目内容
求下列函数的周期(1)y=1-3cos2(
| x |
| 3 |
| π |
| 6 |
(2)y=4sin(3x+
| π |
| 4 |
| π |
| 4 |
分析:(1)利用二倍角公式降次把函数化为一个角的三角函数的形式,然后求出周期.
(1)利用两角和的正弦公式,把函数化为一个角的三角函数的形式,然后求出周期.
(1)利用两角和的正弦公式,把函数化为一个角的三角函数的形式,然后求出周期.
解答:解:(1)y=1-3cos2(
+
)=-
cos(
+
)-
T=
=3π函数的最小正周期是 3π.
(2)y=4sin(3x+
)+3cos(3x+
).=5sin(3x+
+θ)其中tanθ=
它的周期是T=
. 函数的最小正周期是
.
| x |
| 3 |
| π |
| 6 |
| 3 |
| 2 |
| 2x |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
T=
| 2π | ||
|
(2)y=4sin(3x+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 4 |
它的周期是T=
| 2π |
| 3 |
| 2π |
| 3 |
点评:本题考查三角函数的周期性及其求法,考查运算能力,是基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
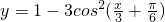 ;
;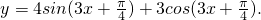
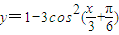 ;
;