题目内容
设A,B两点的坐标分别为(-1,0),(1,0),条件甲: ·
· >0;条件乙:点C的坐标是方程
>0;条件乙:点C的坐标是方程 的解,则甲是乙的( )
的解,则甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
解析试题分析:设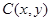 满足条件
满足条件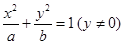 ,则
,则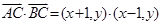
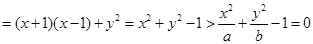 .选
.选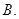
考点:1.必要条件、充分条件与充要条件的判断;2.数量积表示两个向量的夹角.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
2x2-5x-3<0的一个必要不充分条件是( )
A.- <x<3 <x<3 | B.- <x<0 <x<0 | C.-3<x< | D.-1<x<6 |
设 则
则 是“
是“ ”成立的 ( )
”成立的 ( )
| A.充分必要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既非充分也非必要条件 |
命题“所有实数的平方是非负实数”的否定是( )
| A.所有实数的平方是负实数 |
| B.不存在一个实数,它的平方是负实数 |
| C.存在一个实数,它的平方是负实数 |
| D.不存在一个实数它的平方是非负实数 |
下列说法正确的是( )
A.“ 为真”是“ 为真”是“ 为真”的充分不必要条件; 为真”的充分不必要条件; |
B.已知随机变量 ,且 ,且 ,则 ,则 ; ; |
C.若 ,则不等式 ,则不等式 成立的概率是 成立的概率是 ; ; |
D.已知空间直线 ,若 ,若 , , ,则 ,则 . . |
条件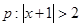 ,条件
,条件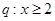 ,则
,则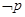 是
是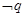 的( )
的( )
| A.充分非必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要的条件 |
设命题p和q,在下列结论中,正确的是( )
①“p∧q”为真是“p∨q”为真的充分不必要条件;
②“p∧q”为假是“p∨q”为真的充分不必要条件;
③“p∨q”为真是“p”为假的必要不充分条件;
④“p”为真是“p∧q”为假的必要不充分条件.
| A.①② | B.①③ |
| C.②④ | D.③④ |
已知命题p:?n∈N,2n>1000,则 p为( )
p为( )
| A.?n∈N,2n≤1000 | B.?n∈N,2n>1000 |
| C.?n∈N,2n≤1000 | D.?n∈N,2n<1000 |
命题“存在一个无理数,它的平方是有理数”的否定是( )
| A.任意一个有理数,它的平方是有理数 |
| B.任意一个无理数,它的平方不是有理数 |
| C.存在一个有理数,它的平方是有理数 |
| D.存在一个无理数,它的平方不是有理数 |