题目内容
 数列{an}的前n项和为Sn,已知Sn=
数列{an}的前n项和为Sn,已知Sn=| n2+3n |
| 2 |
(1)求数列{an}的通项公式;
(2)若bn=bn=
|
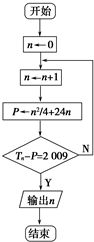
(3)某学生利用第(2)题中的Tn设计了一个程序框图如图所示,但数学老师判断这个程序是一个“死循环”(即程序会永远循环下去,而无法结束).你是否同意老师的观点?请说明理由.
分析:(1)根据n=1时,a1=S1,n≥2时,an=Sn-Sn-1,检验n=1时,是否也满足n≥2时,an=Sn-Sn-1得到的式子,可得数列{an}的通项公式;
(2)根据已知求出数列{bn}的通项公式,利用分组求和法,可得数列{bn}的前n项和为Tn;
(3)根据(2)中前n项和为Tn的表达式,判断循环条件:Tn-P=2009是否会成立,可得答案.
(2)根据已知求出数列{bn}的通项公式,利用分组求和法,可得数列{bn}的前n项和为Tn;
(3)根据(2)中前n项和为Tn的表达式,判断循环条件:Tn-P=2009是否会成立,可得答案.
解答:解:(1)当n=1时,a1=S1=2,
当n≥2时,an=Sn-Sn-1=
-
=n+1,
当n=1时,有a1=1+1=2满足题意,
故数列{an}的通项公式为an=n+1(n∈N*).
(2)当n为偶数时Tn=(b1+b3+…+bn-1)+(b2+b4+…+bn)=(a1+a3+…+an-1)+(22+24+…+2n)
=
•
+
=
+
(2n-1).
当n为奇数时,n+1为偶数,
则Tn+1=
+
(2n+1-1)
=
+
(2n+1-1),
而Tn+1=Tn+bn+1=Tn+2n+1,
∴Tn=
+
•2n+1-
.
(3)由程序框图知,P=
+24n.
设数列{dn}的通项公式为dn=Tn-P(n∈N*),
当n为奇数时,dn=
•2n+1-23n-
,令dn+2-dn=2n+1-46>0,则n≥5,
∴从第5项开始数列{dn}中的奇数项递增,而d1,d3,…,d11均小于2 009且d13>2 009,
∴dn≠2 009.当n为偶数时,dn=
•2n+1-
n-
,令dn+2-dn=2n+2-47>0,则n≥4,
∴从第4项开始数列{dn}中的偶数项递增,而d2,d4,…,d10均小于2 009且d12>2 009,
∴dn≠2 009(n∈N*).故dn≠2 009,即Tn-P≠2 009(n∈N*),
即程序为死循环,所以老师的判断是正确的.
当n≥2时,an=Sn-Sn-1=
| n2+3n |
| 2 |
| (n-1)2+3(n-1) |
| 2 |
当n=1时,有a1=1+1=2满足题意,
故数列{an}的通项公式为an=n+1(n∈N*).
(2)当n为偶数时Tn=(b1+b3+…+bn-1)+(b2+b4+…+bn)=(a1+a3+…+an-1)+(22+24+…+2n)
=
| a1+an-1 |
| 2 |
| n |
| 2 |
| 4(1-2n) |
| 1-4 |
| n2+2n |
| 4 |
| 4 |
| 3 |
当n为奇数时,n+1为偶数,
则Tn+1=
| (n+1)2+2(n+1) |
| 4 |
| 4 |
| 3 |
=
| n2+4n+3 |
| 4 |
| 4 |
| 3 |
而Tn+1=Tn+bn+1=Tn+2n+1,
∴Tn=
| n2+4n+3 |
| 4 |
| 1 |
| 3 |
| 4 |
| 3 |
(3)由程序框图知,P=
| n2 |
| 4 |
设数列{dn}的通项公式为dn=Tn-P(n∈N*),
当n为奇数时,dn=
| 1 |
| 3 |
| 7 |
| 12 |
∴从第5项开始数列{dn}中的奇数项递增,而d1,d3,…,d11均小于2 009且d13>2 009,
∴dn≠2 009.当n为偶数时,dn=
| 2 |
| 3 |
| 47 |
| 2 |
| 4 |
| 3 |
∴从第4项开始数列{dn}中的偶数项递增,而d2,d4,…,d10均小于2 009且d12>2 009,
∴dn≠2 009(n∈N*).故dn≠2 009,即Tn-P≠2 009(n∈N*),
即程序为死循环,所以老师的判断是正确的.
点评:本题考查的知识点是数列求和,程序框图,其中(1)中数列的通项公式是(2)中数列求和的基础,(2)中数列求和又是判断循环条件的基础.

练习册系列答案
相关题目